Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Практична робота № 8
|
|
Тема: Інтегрування тригонометричних функцій.
Мета:Засвоїти методи інтегрування тригонометричних функцій та виробити навички інтегрування.
Теоретичні відомості:
Інтеграли виду 
зводяться до інтегралів від раціональних функцій за допомогою універсальної тригонометричної підстановки:
.
Проте в деяких випадках обчислення 
може бути спрощеним використанням інших підстановок:
1) Якщо 
непарна відносно 
(
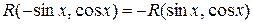), використовується підстановка 
.
2) Якщо 
непарна відносно 
(
), використовується підстановка 
.
3) Якщо парна відносно і , і (
), використовується підстановка 
.
Інтеграли типу 
, де 
і 
– парні додатні числа, обчислюються з допомогою перетворень підінтегральної функції за формулами:
.
Правило 1.
Для обчислення інтегралів виду
та 
(Де п –ціле додатне число), зручно ввести допоміжну функцію sin x в першому випадку та cos x –в другому випадку.
Правило 2.
Для обчислення інтегралів виду
та 
Зручно користуватись формулами
Та вводити допоміжну функцію cos 2x
Правило 3.
Для обчислення інтегралів виду
, (*)
де хоча б одне з чисел-непарне,(якщо т -непарне, то cos x) або sinx (якщо непарне- n)
Правило 4.
Для обчислення інтегралів виду (*), т та n- парні числа зручно користуватись формулами
Правило 5.
Для обчислення інтегралів виду
Зручно користуватись формулами
Приклад 1 Знайти невизначений інтеграл 
.
Розв’язання: Підінтегральна функція 
не є ні непарною відносно , ні непарною відносно , ні парною відносно і , і . Тому будемо використовувати універсальну тригонометричну підстановку. 
Приклад 2. Знайти невизначений інтеграл 
.
Розв’язання:
Підінтегральна функція непарна по , тому використовуємо заміну 
. 
Приклад 3. Знайти невизначений інтеграл
.
Розв’язання:
Підінтегральна функція парна відносно і , і , тому використовуємо підстановку 
.
Правило 6.
Для обчислення інтегралів виду 
, де п - ціле число, більше за 1
Зручно виділити множник tg2x або ctg2x
Завдання до виконання:
Згідно номера в друкованому списку журналу, студенти обирають N (додаванням зводять номер в журналі до однозначного числа), а n та m обчислюються за формулою
n=N+1
m=abc(N-2)
1.
2.
3.
4.
5.
6. 
7. 
8. 
Контрольні запитання:
1. Які методи інтегрування Ви знаєте?
2. В чому полягає суть інтегрування тригонометричних функцій?
3. В яких випадках(при яких значеннях п та т) можливе використання інших методів?
Date: 2015-10-19; view: 331; Нарушение авторских прав