
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Теоретичні відомості
|
|
Література: [5] – с. 449-481, [6] – с. 165-210, [7] – с. 246-266, [8] – с. 167-183.
Монотонність функції. Якщо 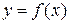 диференційовна на інтервалі
диференційовна на інтервалі 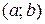 і
і 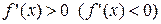 всюди, крім, можливо, скінченого числа точок, в яких
всюди, крім, можливо, скінченого числа точок, в яких 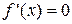 на
на 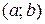 , то функція
, то функція 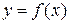 зростає (спадає) на
зростає (спадає) на 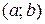 .
.
Інтервали монотонності функції (інтервали спадання чи зростання) відділяються один від одного точками, де похідна функції рівна нулю або не існує. Дані точки називаються критичними точками.
Щоб знайти інтервали монотонності функції 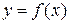 , необхідно: 1) знайти область визначення функції; 2) знайти похідну даної функції; 3) знайти критичні точки з рівняння
, необхідно: 1) знайти область визначення функції; 2) знайти похідну даної функції; 3) знайти критичні точки з рівняння 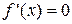 та з умови, що
та з умови, що 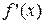 не існує; 4) розділити критичними точками область визначення на інтервали і в кожному з них визначити знак похідної. На інтервалах, де похідна додатна, функція зростає, а де від’ємна – спадає.
не існує; 4) розділити критичними точками область визначення на інтервали і в кожному з них визначити знак похідної. На інтервалах, де похідна додатна, функція зростає, а де від’ємна – спадає.
Локальний екстремум. Достатні умови екстремуму:
Правило 1. Якщо 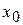 – критична точка функції
– критична точка функції 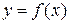 і при довільному малому
і при довільному малому 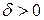 виконуються нерівності
виконуються нерівності 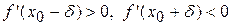 , то функція
, то функція 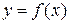 в точці
в точці 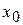 має максимум; якщо ж
має максимум; якщо ж 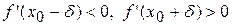 ,то
,то 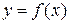 в точці
в точці 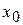 має мінімум; якщо ж знаки
має мінімум; якщо ж знаки 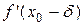 і
і 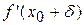 однакові, то функція
однакові, то функція 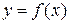 в точці
в точці 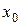 екстремуму не має.
екстремуму не має.
Правило 2. Якщо 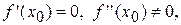 то функція
то функція 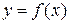 в точці має екстремум, а саме максимум, якщо
в точці має екстремум, а саме максимум, якщо 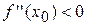 , і мінімум, якщо
, і мінімум, якщо 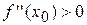 .
.
Для знаходження найбільшого (найменшого) значення функції 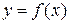 на відрізку
на відрізку  необхідно із значень функції на кінцях відрізка і в критичних точках, які належать даному відрізку, вибрати найбільше (найменше).
необхідно із значень функції на кінцях відрізка і в критичних точках, які належать даному відрізку, вибрати найбільше (найменше).
Приклад 1Знайти найбільше і найменше значення функції 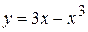 на відрізку
на відрізку 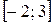 .
.
Розв’язання:
Знайдемо похідну: 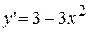 .
.
Знайдемо критичні точки, розв’язавши рівняння 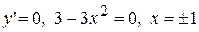 – стаціонарні точки, які належать вказаному відрізку
– стаціонарні точки, які належать вказаному відрізку 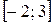 .
.
Визначимо значення функції в стаціонарних точках і на кінцях відрізка:
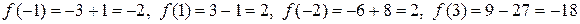 .
.
Із знайдених значень вибираємо найбільше і найменше: 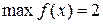 на
на 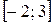 ,
, 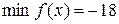 на
на 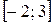 .
.
Опуклість. Увігнутість. Точки перегину. Графік функції 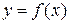 називається опуклим (увігнутим) на інтервалі
називається опуклим (увігнутим) на інтервалі 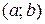 , якщо він розташований нижче (вище) дотичної, проведеної в довільній точці графіка над даним інтервалом.
, якщо він розташований нижче (вище) дотичної, проведеної в довільній точці графіка над даним інтервалом.
Достатні умови опуклості (увігнутості) графіка функції: Якщо 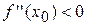 на інтервалі
на інтервалі 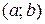 , то графік функції опуклий на вказаному інтервалі; якщо
, то графік функції опуклий на вказаному інтервалі; якщо 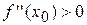 , то графік функції увігнутий на інтервалі
, то графік функції увігнутий на інтервалі 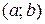 .
.
Точка 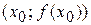 графіка функції, яка відділяє його опуклу частину від увігнутої називається точкою перегину. В абсцисах точок перегину друга похідна функції дорівнює нулю або не існує (
графіка функції, яка відділяє його опуклу частину від увігнутої називається точкою перегину. В абсцисах точок перегину друга похідна функції дорівнює нулю або не існує (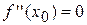 або
або  – не існує). Точки, в яких
– не існує). Точки, в яких 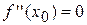 або не існує, називають критичними точками другого роду.
або не існує, називають критичними точками другого роду.
Якщо 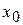 – критична точка другого роду і при довільному достатньо малому
– критична точка другого роду і при довільному достатньо малому 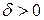 виконуються нерівності
виконуються нерівності 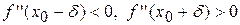 або
або 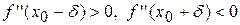 , то точка кривої
, то точка кривої 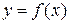 з абсцисою
з абсцисою 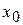 є точкою перегину.
є точкою перегину.
Приклад 2. Знайти проміжки опуклості та ввігнутості графіка функції 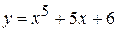 .
.
Розв’язання:
Знайдемо 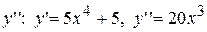 .
.  – критична точка другого роду. Якщо
– критична точка другого роду. Якщо 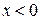 , то
, то 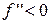 – крива опукла. Якщо
– крива опукла. Якщо 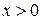 , то
, то  – крива ввігнута. Отже, на проміжку
– крива ввігнута. Отже, на проміжку 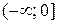 – крива випукла, а на
– крива випукла, а на 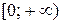 – ввігнута.
– ввігнута.
Асимптоти. Пряма 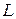 називається асимптотою кривої
називається асимптотою кривої 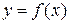 , якщо відстань від точки
, якщо відстань від точки 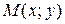 кривої до прямої
кривої до прямої 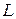 прямує до нуля при необмеженому віддаленні даної точки по кривій від початку координат.
прямує до нуля при необмеженому віддаленні даної точки по кривій від початку координат.
Пряма 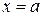 є вертикальною асимптотою кривої
є вертикальною асимптотою кривої 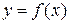 , якщо
, якщо 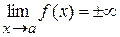 .
.
Пряма 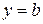 є горизонтальною асимптотою кривої
є горизонтальною асимптотою кривої 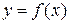 , якщо існує границя
, якщо існує границя 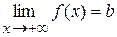 або
або 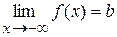 .
.
Пряма 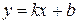 є похилою асимптотою кривої
є похилою асимптотою кривої 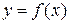 , якщо існують границі:
, якщо існують границі:
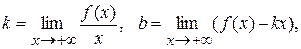
або
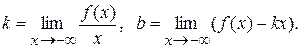
Схема дослідження функції та побудова графіка.
1. Знайти область визначення функції, інтервали неперервності, точки розриву.
2. Знайти (якщо це можливо) точки перетину графіка з координатними осями.
3. Дослідити функцію на періодичність, парність і непарність.
4. Знайти інтервали монотонності, точки локальних екстремумів та значення функції у цих точках.
5. Знайти інтервали опуклості, ввігнутості та перегину.
6. Дослідження функції на межі області існування. Асимптоти графіка.
7. Побудувати графік функції, враховуючи дослідження.
Приклад 3
Дослідити методами диференціального числення функцію
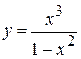
та побудувати її графік
Розв’язання:
1. Область визначення: 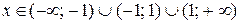 . Точки розриву
. Точки розриву 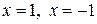 .
.
2. Якщо  , то
, то 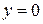 , тому графік перетинає осі координат в точці
, тому графік перетинає осі координат в точці 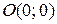 .
.
3. Функція не періодична. Оскільки 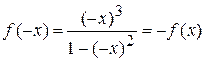 , то функція непарна, а отже графік функції симетричний відносно початку координат.
, то функція непарна, а отже графік функції симетричний відносно початку координат.
4. 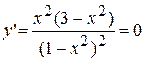 . Розв’язками даного рівняння є
. Розв’язками даного рівняння є 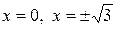 . Похідна не існує в
. Похідна не існує в 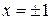 . Знайдемо знаки
. Знайдемо знаки  на проміжках:
на проміжках:
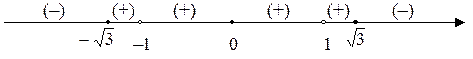
Отже, на 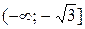 – функція спадає,
– функція спадає,
на 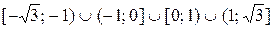 – функція зростає,
– функція зростає,
на 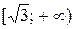 – функція спадає.
– функція спадає.
У точках 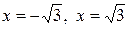 функція має локальний екстремум:
функція має локальний екстремум: 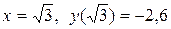 – локальний максимум,
– локальний максимум, 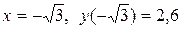 – локальний мінімум.
– локальний мінімум.
5. Знаходимо 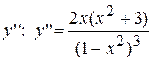 . Похідна
. Похідна 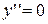 при
при  і не існує при
і не існує при 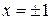 . Знайдемо знаки
. Знайдемо знаки 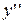 на проміжках:
на проміжках:
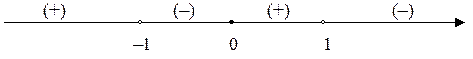
Отже, на 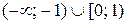 – крива ввігнута, на
– крива ввігнута, на 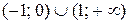 – крива опукла.
– крива опукла.
6. 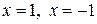 – вертикальні асимптоти кривої. Знайдемо похилу асимптоту кривої
– вертикальні асимптоти кривої. Знайдемо похилу асимптоту кривої 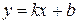 .
.
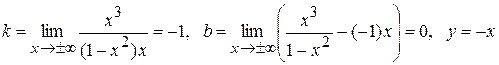 – похила асимптота.
– похила асимптота.
7. Враховуючи проведені дослідження будуємо графік функції.

Завдання до виконання:
1.Дослідити функції та побудувати їх графіки.
2. Знайти найменше та найбільше значення даної функції на проміжку[-3;4] (Завдання обираються відповідно порядкового номера прізвища студента в друкованому списку журналу):
1. 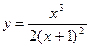 14.
14. 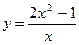
2. 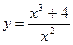 15.
15. 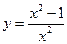
3. 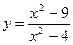 16.
16. 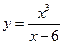
4. 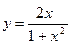 17.
17. 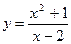
5. 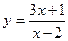 18.
18. 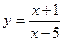
6. 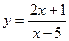 19.
19. 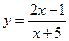
7. 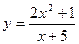 20.
20. 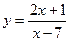
8. 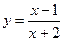 21.
21. 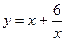
9. 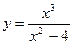 22.
22. 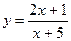
10. 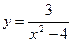 23.
23. 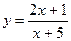
11. 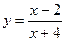 24.
24. 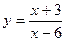
12. 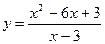 25.
25. 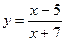
13. 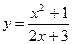 26.
26. 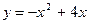
27. 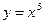 29.
29. 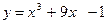
28. 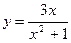 30.
30. 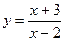
Контрольні запитання:
1. Дати означення області визначення функції та області значень функції.
2. Навести класифікацію точок розриву.
3. В яких точках можуть існувати вертикальні асимптоти?
4. Як знайти похилі асимптоти?
5. Дати означення парної (непарної) функції.
6. Дати означення періодичної функції. Навести приклади періодичних функцій.
7. Дати означення критичних точок першого та другого роду.
8. Як знайти проміжки монотонності та екстремуми функції?
9. Як знайти проміжки опуклості та угнутості функції та точки перегину?
10. Як знайти точки перетину графіка функції з осями координат?
Date: 2015-10-19; view: 464; Нарушение авторских прав