
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Приклад 1. Розв’язати систему лінійних рівнянь
|
|

трьома способами:
а) методом Крамера;
б) матричним способом;
в) методом Гаусса.
Розв’язання.
Обчислимо визначник системи:

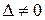 , тому розв’язок можна знайти за формулами Крамера та матричним способом.
, тому розв’язок можна знайти за формулами Крамера та матричним способом.
а) Знайдемо  :
:



Підставляючи знайдені значення визначників у формули Крамера (4) отримаємо



б) Знайдемо розв’язок матричним способом. Відповідно до введених позначень маємо
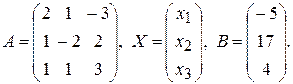
Використаємо отримане в попередньому пункті значення визначника матриці 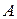 :
:
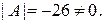
Для знаходження оберненої матриці  обчислимо алгебраїчні доповнення елементів матриці
обчислимо алгебраїчні доповнення елементів матриці 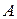 :
:





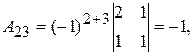



Згідно формули (1)  має вигляд
має вигляд

Розв’язок системи знайдемо за формулою (3):
 звідки випливає, що
звідки випливає, що  ,
, 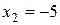 ,
,  .
.
Завдання до виконання:
1.Транспонувати матрицю В;
2.Знайти матрицю А-1
1. А= 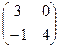 В=
В= 
2. А= 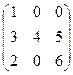 В=
В= 
3. А=  В=
В= 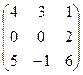
4. А=  В=
В= 
5. А= 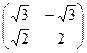 В=
В= 
6. А= 
 В=
В= 
7. А=  В=
В= 
8. А=  В=
В= 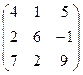
9. А= 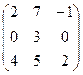 В=
В= 
10. А=  В=
В= 
11. А= 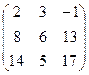 В=
В= 
12. А=  В=
В= 
13. А=  В=
В= 
14. А=  В=
В= 
15. А= 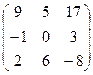 В=
В= 
16. А=  В=
В= 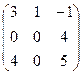
17. А= 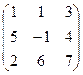 В=
В= 
18. А=  В=
В= 
19. А=  В=
В= 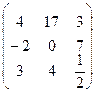
20. А=  В=
В= 
21. А=  В=
В= 
22. А=  В=
В= 
23. А=  В=
В= 
24. А=  В=
В= 
25. А= 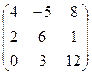 В=
В= 
26. А=  В=
В= 
27. А=  В=
В= 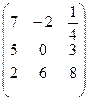
28. А=  В=
В= 
29. А=  В=
В= 
30. А= 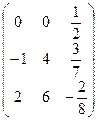 В=
В= 
3. Розв’язати систему лінійних рівнянь методами:
· Крамера;
· Гауса;
· Матричним методом.
| №1 | 
| №2 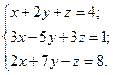
| |
| №3 | 
| №4 
| |
| №5 | 
| №6 
| |
| №7 | 
| №8 
| |
| №9 | 
| №10 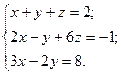
| |
| №11 | 
| №12 
| |
| №13 | 
| №14 
| |
| №15 | 
| №16 
| |
| №17 | 
| №18 
| |
| №19 | 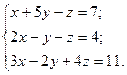
| №20 
| |
| №21 | 
| №22 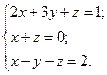
| |
| №23 | 
| №24 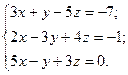
| |
| №25 | 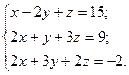
| №26 
| |
| №27 | 
| №28 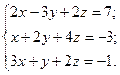
| |
| №29 | 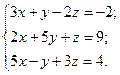
| №30 
|
Контрольні запитання:
1. Що таке матриця?
2. Як додати матриці?
3. Записати формулу множення матриць?
4. В чому полягає метод Гауса?
5. В чому полягає метод Крамера?
6. Записати формули для розв’язання системи лінійних рівнянь матричним способом.
7. Яка матриця називається транспонованою?
Date: 2015-10-19; view: 442; Нарушение авторских прав