Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Алгоритм построения обратной матрицы
|
|
1) Найти определитель заданной матрицы.
2) Для всех элементов матрицы вычислить алгебраические дополнения.
3) Составить матрицу из соответствующих алгебраических дополнений.
4) Транспонировать матрицу из алгебраических дополнений и получить присоединённую матрицу 
.
5) Построить обратную матрицу из присоединённой, умножением её на число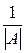 
по формуле 
.
6) Проверить правильность выполненных действий по определению 
.
Пример 2.11. Найти обратную матрицу для матрицы 
Решение. Вычислим определитель матрицы 
, 
, следовательно, заданная матрица имеет обратную (по теореме).
Найдем алгебраические дополнения элементов матрицы
, 
, 
,
, 
, 
,
, 
, 
.
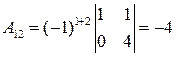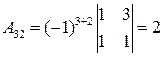Составим матрицу из алгебраических дополнений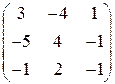 
, затем транспонируем ее и получаем присоединённую матрицу 
. Обратная матрица получается умножением присоединённой матрицы на величину 
, 
.
Проверка правильности вычислений обратной матрицы производится в соответствии с равенством .
Date: 2015-10-19; view: 491; Нарушение авторских прав