Производная непрерывного отображения

В теории оптимизации вводимые далее понятия производных играют первостепен-

ную роль, т. к. позволяют, помимо всего прочего, обобщить на бесконечномерный

случай многие традиционные конструкции конечномерного анализа, такие, как

градиентные методы, методы Ньютона, матрицы Якоби и т. д.

Сделаем вначале общие замечания о дальнейшем изложении.

В функциональном анализе дифференциальное исчисление может рассматривать-

ся для отображений одного аффинного пространства в другое, причем первое

считается нормированным. При этом вводится специальное понятие аффинного

пространства и присоединенного к нему векторного пространства. Грубо говоря,

аффинное пространство — это пространство "свободных" векторов, имеющих

начало и конец в любых точках. В векторном же пространстве все векторы начи-

наются в нуле. Нетрудно показать, что векторное пространство является частным

случаем аффинного пространства. Для этого достаточно сопоставить любым двум

векторам вектор их разности.

В соответствии с последним замечанием можно рассматривать (менее общую) теорию

дифференциального исчисления для отображений векторного пространства в вектор-

ное же пространство. Чаще всего эти векторные пространства наделяются структурой

банахова пространства. Далее мы будем следовать именно такому подходу.

В функциональном анализе рассматривают два вида дифференцируемости: сильную,

или дифференцируемость по Фреше, и слабую — дифференцируемость по Гато. Пер-

вый случай соответствует понятию полной производной, а второй — понятию произ-

водной по направлению (или частной производной вдоль вектора). Мы далее в ос-

новном изложим лишь теорию сильной дифференцируемости, а потому вообще не

будем употреблять прилагательных "сильная" и "слабая" для производных.

Пусть E и F — банаховы (действительные) пространства, A E — открытое под-

множество в E. Пусть также f: A 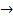F, g: A 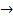F — заданные непрерывные ото-

бражения. Отображения f и g называются касательными в точке ,если

(Отсюда следует, что f .)

Легко показать, что это отношение эквивалентности во множестве непрерывных

отображений A 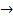F, т. е., в частности, если f и g касательны в точке и g и h касательны в точке , то и f и h касательны в точке . x

Непрерывное отображение f: A 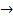F называется дифференцируемым в точке ,

если существует линейное отображение u: E 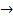F, такое, что отображение E 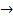F вида

касательно к f в точке . Такое линейное отображение называется производной

(или полной производной) отображения f в точке и обозначается символом

или Df .

Можно доказать, что если производная существует, то она единственна. Действи-

тельно, пусть найдутся два таких отображения:

Эти отображения по предположению касательны к fx при x= . (Они также

будут касательными между собой.) Для линейного отображения это означает, что

(1.4)

Если , т. е. тождественного равенства нет, то для некоторого

Отсюда следует, что при

и соотношение (1.4) не может быть выполнено

Теорема 1.20. Если непрерывное отображение f: A 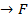дифференцируемо в точке , то производная

является непрерывным линейным отображением .

Date: 2015-10-18; view: 748; Нарушение авторских прав