Евклидовы пространства

В евклидовых пространствах вводится понятие скалярного произведения, а уже на

его основе определяется норма.

Пусть в действительном линейном пространстве L задан функционал .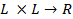

Значение этого функционала называется скалярным произведением и обозначается x,y

если выполняются следующие условия:

1.

2.

3.

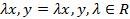
4.

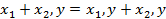
5.

Линейное пространство с заданным в нем скалярным произведением называется

евклидовым пространством. Иногда евклидовы пространства называются предгиль-

бертовыми пространствами, а для скалярного произведения используется обозна-

чение .

Норма в евклидовом пространстве вводится формулой

Можно проверить, что все аксиомы нормы оказываются при этом выполненными.

В евклидовом пространстве может быть задан угол между векторами. Для ненуле-

вых векторов x L,y угол 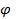определяется выражением

cos =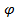

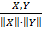
Можно доказать, что, как и должно быть, правая часть равенства не превосходит

единицы.

Если для ненулевых векторов x L,y имеем x, y =0, то 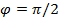, а векторы

x и y называются ортогональными.

Система ненулевых векторов из L называется ортогональной, если они попар-

но ортогональны:

Счетность множества не предполагается.

Date: 2015-10-18; view: 283; Нарушение авторских прав