Упражнение 1.6

Доказать, что если векторы ортогональны, то они линейно независимы.

Если система векторов (семейство элементов) ортогональна и полна в L, то

она называется ортогональным базисом пространства L. Если при этом

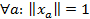, то имеем ортогональный нормированный базис или ортонормальный

базис. Если — ортогональная система, то — ортонормальная.

Примеры евклидовых пространств.

1. Пространство действительных чисел R. Скалярное произведение — обычное

произведение действительных чисел.

2. 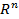— n - мерное арифметическое пространство с элементами вида, 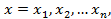где — действительные числа. Операции сложения и умножения на числа — общеизвестны, а скалярное произведение задается соотношением,

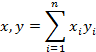
3. Линейное пространство 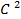a, b непрерывных на a, b действительных функ-

ций со скалярным произведением

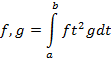
является евклидовым пространством. Можно установить, что все аксиомы ска-

лярного произведения оказываются выполненными.

В этом случае норма, очевидно, задается выражением

Индуцированная этой нормой метрика имеет вид

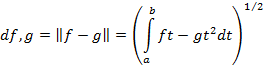
что совпадает с ранее введенной метрикой при наделении данного множества

функций структурой метрического пространства и выборе обозначения a, b.

Одним из ортогональных базисов пространства a, b является тригонометрическая система функций:

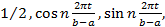n=1,2,….,

4. Ранее рассматривалось также метрическое пространство a, b с метрикой

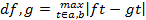
Норма определялась формулой

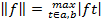
(Было установлено, что это банахово пространство.)

Поставим вопрос, можно ли наделить данное нормированное пространство

структурой евклидова пространства. Для этого достаточно задать вышеприве-

денную норму с помощью некоторого скалярного произведения:

Можно показать, что ответ будет отрицательным. Норму пространства C a, b нель-

зя задать с помощью скалярного произведения. Таким образом, не все нормирован-

ные пространства можно "превратить" в евклидовы пространства. Евклидовы про-

странства составляют лишь часть нормированных пространств. Еще раз отметим, что

пространство C a, b дает пример банахова, но не евклидова пространства.

Можно доказать следующее утверждение (характеристическое свойство евклидовых пространств).

Теорема 1.8. Для того чтобы нормированное пространство L было евклидовым, необходимо и достаточно, чтобы для 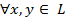выполнялось равенство

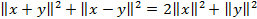
Доказательство опускаем.

Теорема 1.9 (процесс ортогонализации Шмидта). Пусть

есть линейно независимая (счетная) система векторов в евклидовом пространстве

L. (Ясно, что в эту систему не могут входить нулевые векторы, иначе получим ли-

нейную зависимость). Тогда в L существует система векторов

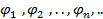
Такая что

1. 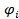-ортонормальна

2. 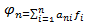причем

(Переход от линейно независимой системы векторов к ортогональной называет-

ся процессом ортогонализации.)

Доказательство. Положим

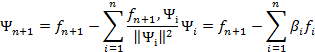
В этом случае вектор 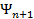будет ортогонален всем векторам 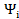, i= 1,...,. n Дейст-

вительно,

Для n=1 имеем

Но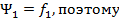

,

Установлена ортогональность 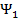и 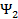. Покажем по индукции, что система векто-

ров ,.., ,.., построенная согласно выражению (1.3), ортогональна.

Пусть ,.., ,.., уже построены и ортогональны. Покажем, что тогда вектор ,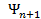

будет ортогонален всем 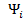,.., 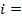1,..., n

Имеем (для любого фиксированного j =1,.., n:

(Очевидно, в данном выражении только одно слагаемое суммы не равно нулю,

а именно слагаемое с индексом i= j. Остальные слагаемые равны нулю, т. к.,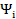

i= 1,..., n ортогональны и 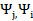=0, i j.)

Последнее соотношение может выполняться и если в результате процедуры (1.3)

будут все время получаться нулевые векторы. Покажем, что это невозможно из-за

линейной независимости системы векторов Действительно, пусть

получили, 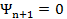тогда

что противоречит линейной независимости . Следовательно . Для окончательного доказательства теоремы достаточно положить

Теорема доказана.

Date: 2015-10-18; view: 313; Нарушение авторских прав