Гильбертовы пространства

Гильбертовым пространством называется полное евклидово пространство. (На-

помним, что понятие полноты уже вводилось нами ранее для метрических про-

странств.) Таким образом, гильбертовы пространства — это частный случай евкли-

довых (предгильбертовых) пространств. В то же время гильбертово пространство

дает пример полного линейного нормированного пространства (со специфической

нормой) и поэтому является частным случаем банахова пространства. Ясно, что

евклидово пространство не обязано быть банаховым, т. к. оно может быть неполно.

Иногда при определении гильбертова пространства выдвигается дополнительное

требование бесконечномерности, т. е. существования любого числа линейно неза-

висимых элементов. Мы таких предположений не делаем и, следовательно, допус-

каем существование конечномерных гильбертовых пространств. Кроме того, часто

при изучении гильбертовых пространств явно или неявно предполагают их сепара-

бельность.

Можно показать, что любое конечномерное евклидово пространство является гиль-

бертовым (т. е. полно).

Изоморфизмом евклидова пространства L на евклидово пространство L называет-

ся биективное отображение 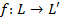такое, что

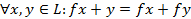
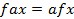
Таким образом, изоморфизм есть такое взаимно однозначное соответствие, которое

сохраняет как линейные операции, определенные в пространствах L, 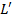, так и ска-

лярное произведение. Евклидовы пространства называются изоморфными, если

можно построить соответствующий изоморфизм f.

Рассмотрим конечномерные (n -мерные) евклидовы пространства, т. е. такие линей-

ные пространства со скалярным произведением, для которых существует конечное

число n линейно независимых векторов, а любые n+ 1 векторов — линейно зави-

симы. Можно доказать, что любые два n -мерных евклидова пространства изоморф-

ны между собой. Следовательно, любое такое пространство изоморфно арифмети-

ческому пространству 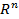(состоящему из наборов n действительных чисел). Если

в каком-нибудь n -мерном евклидовом пространстве 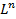доказана теорема, сфор-

мулированная в терминах операций сложения, умножения на числа и скалярного

произведения векторов, то эта же теорема верна и в любом изоморфном ему про-

странстве. В качестве такого "стандартного" пространства часто используется

пространство .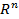

Евклидовы пространства бесконечного числа измерений не обязаны быть изоморф-

ными между собой.

Для гильбертовых пространств в общем случае справедливо следующее утвержде-

ние.

Теорема 1.11. Если два бесконечномерных гильбертова пространства сепарабель-

ны, то они изоморфны между собой.

(Напомним, что метрическое пространство E называется сепарабельным, если в E

существует не более чем счетное (т. е. конечное или счетное) всюду плотное мно-

жество.)

Доказательство этой теоремы проводить не будем. Отметим только, что оно за-

ключается в установлении изоморфизма любого бесконечномерного сепарабельно-

го гильбертова пространства евклидову пространству 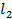бесконечных последова-

тельностей действительных чисел:

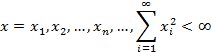
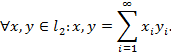
(Здесь ряд в правой части выражения для скалярного произведения сходится. Можно

показать, что евклидово пространство является примером сепарабельного бес-

конечномерного гильбертова пространства.)

Аналогично пространству 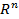в случае конечного числа измерений, в бесконечно-

мерном случае пространство 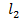является "стандартным" гильбертовым пространст-

вом. Можно сказать более определенно. С точностью до изоморфизма существует

только одно сепарабельное бесконечномерное гильбертово пространство. Кон-

цепция сепарабельности в теории гильбертовых пространств настолько важна, что

требование сепарабельности часто изначально включается в определение гильбер-

това пространства и отдельно затем не оговаривается.

Date: 2015-10-18; view: 636; Нарушение авторских прав