Линейные пространства

Часто приходится встречаться с объектами, над которыми производятся операции

сложения и умножения на числа. Например, векторы в геометрии в трехмерном

пространстве умножаются на числа и складываются. Вещественные функции веще-

ственных аргументов умножаются на числа и складываются и т. п. Одни и те же

операции производятся над совершенно разными объектами. Для того чтобы изу-

чить все такие примеры с единой точки зрения, вводится понятие линейного (или

векторного) пространства.

Пусть на множестве L элементов, x y, z, … заданы два отображения:

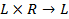
где R — множество действительных чисел ("вещественная прямая"). Обозначим эти

отображения как:

соответственно.

Тогда множество L называется действительным линейным пространством, если

для введенных отображений выполнены следующие требования:

1. 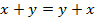(коммутативность).

2 (ассоциативность).

3. (существование нуля).

4. Для (существование противоположного элемента).

5. 1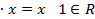

6.

7.

8.

Часто говорят о линейном векторном пространстве. Сами элементы L также назы-

ваются векторами.

Если вместо множества R действительных чисел используется множество C ком-

плексных чисел, то получим комплексное линейное пространство.

Непустое подмножество линейного пространства L называется подпространством,

если оно само является линейным пространством по отношению к определенным

в L операциям.

Пусть — произвольное непустое семейство элементов линейного пространст-

ва L (счетность множества не предполагается). Определение понятия семейства

элементов было дано выше. Рассмотрим все подпространства линейного пространст-

ва L, содержащие заданную систему векторов . Пересечение этих подпро-

странств, очевидно, тоже будет подпространством. Это так называемое наименьшее

подпространство, содержащее . Оно называется подпространством, порожден-

ным множеством, или линейной оболочкой семейства элементов .

Примеры линейных пространств.

1. Множество R действительных чисел с обычными операциями сложения и умно-

жения (L совпадает с R).

2. Совокупность систем n действительных (или комплексных) чисел

, где сложение и умножение на число определяются формулами

называется n -мерным арифметическим пространством и обозначается n

(для действительного пространства) или (в комплексном случае).

3. Множество непрерывных на отрезке a, b функций с обычными операциями

сложения и умножения на числа образует векторные пространства C a, b, a, b

Конечное множество векторов называется линейно зависимым, если существует

множество чисел , из которых не все равны нулю, такое, что .Если

то конечное множество называется линейно независимым.

Замечание. Важно, что линейная зависимость и линейная независимость — свой-

ства множества векторов. Однако соответствующие прилагательные часто условно

применяются к самим векторам, которые называются линейно зависимыми или ли-

нейно независимыми.

Множество X (не обязательно конечное) называется линейно независимым, если

линейно независимо любое его конечное подмножество. В противном случае мно-

жество X — линейно зависимо.

Если — конечное множество и для некоторого справедливо представле-

ние 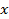= , то говорят, что x является линейной комбинацией векторов .

Линейное пространство L называется конечномерным, если в нем существует n ли-

нейно независимых векторов, а любые n +1 векторы — линейно зависимы. В этом

случае говорят, что L имеет размерность n. Любой набор из n линейно независи-

мых векторов n -мерного пространства L называется базисом этого пространства.

Если существует любое количество линейно независимых векторов, то пространст-

во L называется бесконечномерным. Понятие базиса бесконечномерного простран-

ства здесь не обсуждается.

Date: 2015-10-18; view: 317; Нарушение авторских прав