Банаховы пространства

Линейное пространство L называется нормированным, если на L задан функционал

, удовлетворяющий следующим четырем условиям для,

1.

2.

3.

4. (неравенство треугольника).

Такой функционал f называется нормой в L. Значение f x обозначается и на-

зывается нормой элемента x. Нормированным пространством называется линей-

ное пространство L с заданной в нем нормой.

Если — норма в L, то функционал вида есть

расстояние в L. Норма индуцирует соответствующую метрику. Справедливость ак-

сиом метрики легко проверяется.

Таким образом, для нормированных пространств имеют смысл все понятия, вве-

денные для метрических пространств. Полное нормированное пространство назы-

вается банаховым пространством или B -пространством.

Пример 1. В пространстве C a, b непрерывных функций определим норму фор-

мулой:

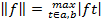
Порожденная этой нормой метрика совпадает с ранее рассматриваемой метрикой

для этого множества. Как мы указывали, это множество функций является полным

относительно своей метрики, и, следовательно, пространство C a, b является ба-

наховым пространством.

Подпространством нормированного пространства L называется подпространство

линейного пространства L (линейное подпространство), которое является замкну-

тым множеством относительно расстояния, индуцированного заданной нормой.

Иначе говоря, подпространство нормированного пространства есть линейное под-

пространство, содержащее все свои предельные точки. Еще раз отметим, что толь-

ко замкнутые линейные подпространства нормированного пространства будут на-

зываться подпространствами нормированного пространства.

Например, в пространстве C a, b непрерывных функций с указанной нормой

многочлены образуют подпространство соответствующего линейного пространст-

ва, но не замкнутое. Следовательно, это подпространство не будет подпространст-

вом нормированного пространства C a, b. В конечномерном нормированном про-

странстве ситуация проще. Там любое линейное подпространство обязательно

замкнуто.

Совокупность элементов (не обязательно замкнутую), содержащую вместе с x, y их

произвольную линейную комбинацию (подпространство линейного простран-

ства), будем в случае нормированных пространств называть линейным многообразием.

Для нормированных пространств, являющихся частным случаем линейных про-

странств, сохраняются все определения и результаты, полученные для линейных

пространств. Например, такие понятия, как наименьшее подпространство, порож-

денное подпространство, линейная оболочка и т. д.

В теории нормированных пространств замыкание линейной оболочки произволь-

ного непустого множества называется подпространством, порожденным эле-

ментами . (Можно доказать, что указанное замыкание действительно будет

линейным подпространством.)

Система элементов нормированного пространства L называется полной, если по-

рождаемое ею линейное многообразие имеет замыкание, совпадающее со всем про-

странством L. Иначе говоря, если порождаемое ею подпространство совпадает с L.

Пример 2. Система функций 1,t,

полна в пространстве непрерывных функций C a, b.

Date: 2015-10-18; view: 426; Нарушение авторских прав