Метрические пространства

В теории метрических пространств развивается геометрический язык, на котором

выражаются результаты анализа. Этот язык позволяет придать этим результатам

достаточную общность и вместе с тем дать наиболее простые и отражающие суть

дела доказательства. Нас будут интересовать топологические аспекты теории мет-

рических пространств, связанные с концепцией предельного перехода, а также ал-

гебраические аспекты при изучении основных операций над элементами метриче-

ских пространств. Метрические пространства являются частным видом более об-

щих топологических пространств.

Пусть Е — некоторое множество. Расстояние в Е есть отображение (функционал)

d произведения во множество действительных чисел R:

Предполагается, что функционал d обладает следующими свойствами:

1.

2.

3.

4.

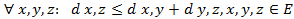
. Свойство 4 называется неравенством треугольника.

Множество Е с заданным в нем расстоянием d называется метрическим простран-

ством. Обычно это пространство, т. е. пару E, d, обозначают одной буквой Е.

Примеры метрических пространств.

1. Множество C a, b всех непрерывных действительных функций, определенных

на отрезке a, b, с расстоянием

2. В этом же множестве функций можно ввести расстояние

В результате получим пространство непрерывных функций с квадратичной метри-

кой a, b.

Обычно та или иная метрика для построения метрического пространства выбирает-

ся в соответствии с особенностями решаемой задачи. Первая метрика в приведен-

ном примере отражает достаточно жесткое требование к близости функций.

Ее применяют, например, при решении задачи равномерного приближения функ-

ций (равномерная аппроксимация), когда требуется гарантировать, чтобы на всем

отрезке a, b отклонение функций f и g было меньше некоторой заданной величи-

ны. Вторая метрика отражает менее жесткое требование. Оно заключается в том,

что для "подавляющего" большинства (но не для всех) значений аргумента t из

a, b абсолютная величина также мала. Во многих случаях, например, при

обработке результатов наблюдений квадратичное приближение является наиболее

приемлемым, т. к. оно позволяет сглаживать отдельные локальные выбросы ап-

проксимируемой (экспериментальной) функции с помощью некоторой теоретиче-

ской расчетной зависимости. В итоге можно получить достаточно точное общее

представление о характере протекающего процесса даже при наличии ошибок при

измерении экспериментальных зависимостей.

Date: 2015-10-18; view: 361; Нарушение авторских прав