Функции и отображения

Операции над множествами и их свойства

Объединение множеств:

Здесь v - знак логического "ИЛИ".

Пересечение множеств:

Коммутативность операций объединения и пересечения множеств:

Ассоциативность операций и :

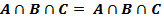
Дистрибутивность:

Разность множеств:

Декартово произведение множеств:

Функции и отображения

Отношение называется отображением X в Y или функцией, определен-

ной в X и принимающей значения в Y, если для x:

Если 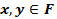, то элемент y называется значением F в x и обозначается как .

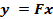Используются также обозначения:

Принципиально важным свойством отображения является то, что любому значе-

нию "аргумента" x ставится в соответствие единственный элемент y. Такое понятие, как "многозначная" функция, здесь не рассматривается. Вполне правомерно, ко-

нечно, определить отображение, значениями которого являются подмножества не-

которого данного множества, состоящие более чем из одного элемента. Но такое

определение практически бесполезно, т. к. не удается разумным образом опреде-

лить алгебраические операции над значениями таких функций. Например, операция

извлечения корня из вещественного числа 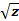приводит к двум значениям со зна-

ками "плюс" и "минус". Но тогда как понимать равенство: ? Левая

часть имеет три разных значения, а правая — только два. (Хотя, конечно, сущест-

вует и понятие Римановой поверхности.)

Сделаем еще одно замечание. Обычно (в "школьной" математике) различают

понятия функции и ее графика. В данном выше определении эти понятия со-

впадают.

В современной математике важнейшую роль играет рассмотрение отображения

(функции) как единого объекта (такого же, как точка или число) и проведение яс-

ного различия между отображением F и любым из его значений F x. Первое есть

элемент множества отображений X в Y, обозначаемого как , второе — элемент множества Y, причем

Таким образом, отображение F есть некоторое множество упорядоченных пар x, y.

Пусть .Пусть также . Тогда множество

называется образом множества А при отображении F. Здесь 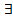— квантор сущест-

вования. x читается: существует х. Прообразом множества B Y при отображе-

нии F называется множество

Пусть .Пусть .Тогда множество

называется сужением отображения F на множестве А.

Date: 2015-10-18; view: 621; Нарушение авторских прав