Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

I. Показательные уравнения
|
|
Простейшее показательное (неизвестная величина находится в показателе) имеет вид ax = b, где a > 0, a ≠ 1.
Если b ≤ 0, то уравнение решений не имеет.
Если b > 0, то уравнение имеет единственное решение  .
.
Уравнение af(x) = ag(x), где a > 0, a ≠ 1, равносильно уравнению f(x) = g(x).
При решении более сложных показательных уравнений применяются как традиционные методы: разложение на множители, замена переменной (в том числе для сведения уравнения к квадратному), так и логарифмирование обеих частей по нужному основанию.
Пример 1. Решить уравнение:  .
.
 ; так как основания выражений в правой и в левой частях одинаковы, то для выполнения равенства, необходимо равенство показателей степени, то есть x = 3.
; так как основания выражений в правой и в левой частях одинаковы, то для выполнения равенства, необходимо равенство показателей степени, то есть x = 3.
Ответ: 3.
Пример 2. Решить уравнение:  .
.
Данное уравнение не имеет решений, так как область значений любой показательной функции  , то есть не может принимать отрицательных значений.
, то есть не может принимать отрицательных значений.
Ответ: Æ.
Пример 3. Решить уравнение: 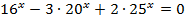 .
.
После несложных преобразований данное уравнение принимает вид однородного уравнения второй степени:  , которое после деления обеих частей на
, которое после деления обеих частей на  принимает вид:
принимает вид:  .
.
Заметим, что деление на  корректно, так как при любом xÎ R 5 x > 0 (по свойству показательной функции).
корректно, так как при любом xÎ R 5 x > 0 (по свойству показательной функции).
Далее, вводим новую переменную 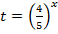 и получаем квадратное уравнение:
и получаем квадратное уравнение:
 Þ
Þ 
После обратной замены получаем 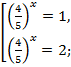 Þ
Þ 
Ответ:  .
.
II. Показательные неравенства.
При решении показательных неравенств необходимо учитывать характер монотонности показательной функции в зависимости от основания.
Простейшее показательное неравенство af(x) ≤ ag(x) при a > 1 равносильно неравенству f(x) ≤ g(x), а при 0 < a < 1 неравенству f(x) ≥ g(x).
Пример 1. Решить неравенство:  .
.
Данное неравенство не имеет решений, так как показательная функция при любом x принимает только положительные значения.
Ответ: Æ.
Пример 2. Решить неравенство:  .
.
Данное неравенство всегда верно, так как показательная функция при любом x принимает только положительные значения.
Ответ: (– ∞; + ∞).
Пример 3. Решить неравенство: 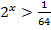 .
.
 , функция 2 x – возрастающая, так как 2 > 1;
, функция 2 x – возрастающая, так как 2 > 1;
x > – 6.
Ответ: (– 6; + ∞).
Пример 4. Решить неравенство:  .
.
 , функция
, функция  – убывающая, так как
– убывающая, так как  ;
;
x ≤ 6.
Ответ: (– ∞; 6].
III. Логарифмические уравнения.
Простейшее логарифмическое уравнение имеет вид  , где a > 0, a ≠ 1.
, где a > 0, a ≠ 1.
Оно имеет единственное решение x = ab.
Уравнение вида  , где a > 0, a ≠ 1 равносильно системе
, где a > 0, a ≠ 1 равносильно системе

Таким образом, логарифмические уравнения можно решать, находя ОДЗ с целью отбрасывания возможных посторонних корней, или выполняя ПРОВЕРКУ, подставляя найденные корни в исходное уравнение.
Пример 1. Решить уравнение:  .
.
2 x – 1 = 52, 2 x - 1 = 25, x = 13.
В данном примере находить ОДЗ или делать проверку необязательно, так как требование 2 x – 1 > 0 выполняется автоматически.
Ответ: 2,5.
Пример 2. Решить уравнение:  .
.
ОДЗ уравнения: x > 0.Данное уравнение с помощью замены  приводится к квадратному уравнению:
приводится к квадратному уравнению:  , корни которого t 1 = 1 и t 2 = 2.
, корни которого t 1 = 1 и t 2 = 2.
Делаем обратную замену и решаем совокупность простейших логарифмических уравнений:
 или
x = 10 или
x = 10
|  ;
x = 100 ;
x = 100
|
Оба корня входят в ОДЗ.
Ответ: 10;100.
IV. Логарифмические неравенства.
При решении логарифмических неравенств необходимо учитывать характер монотонности соответствующей функции в зависимости от её основания (функция  убывает при 0 < a < 1, возрастает при a > 1).
убывает при 0 < a < 1, возрастает при a > 1).
Неравенство 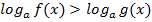 равносильно системе неравенств:
равносильно системе неравенств:
 при a > 1
при a > 1  при 0 < a < 1.
при 0 < a < 1.
Обобщая, получим: неравенство  равносильно совокупности систем неравенств:
равносильно совокупности систем неравенств:
 или
или 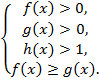
Пример. Решить неравенство:  .
.
 .
.
Данное неравенство равносильно системе неравенств:


|
        
 
|
 .
.
Ответ:  (ответ можно записать в виде
(ответ можно записать в виде  ).
).
|
1 уровень
233. Решите уравнения:
а)  ; б)
; б)  ; в)
; в)  ;
;
г)  ; д)
; д)  ; е)
; е)  ;
;
ж)  ; з)
; з)  ; и)
; и) 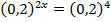 .
.
234. Решите уравнения:
а)  ; б)
; б)  ; в)
; в)  ;
;
г)  ; д)
; д)  ; е)
; е)  ;
;
ж)  ; з)
; з) 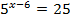 ; и)
; и)  .
.
235. Решите неравенства:
а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  ;
;
д) 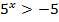 ; е)
; е)  ; ж)
; ж)  ; з)
; з)  .
.
236. Решите неравенства:
а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  ;
;
д)  ; е)
; е)  ; ж)
; ж)  ; з)
; з)  .
.
237. Решите уравнения:
а)  ; б)
; б)  ; в)
; в) 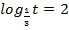 ; г)
; г)  ;
;
д)  ; е)
; е)  ; ж)
; ж)  ; з)
; з)  .
.
238. Решите уравнения:
а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  ;
;
д)  ; е)
; е)  ; ж)
; ж)  ; з)
; з)  .
.
239. Решите неравенства:
а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  ;
;
д)  ; е)
; е)  ; ж)
; ж) 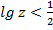 ; з)
; з)  .
.
240. Решите неравенства:
а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  ;
;
д) 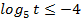 ; е)
; е) 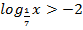 ; ж)
; ж)  ; з)
; з)  .
.
2 уровень
241. Решите уравнения:
а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  ;
;
д)  ; е)
; е)  ; ж)
; ж)  ; з)
; з)  ;
;
и)  ; к)
; к) 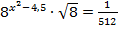 ; л)
; л) 
242. Решите уравнения:
а)  ; б)
; б)  ; в)
; в)  ; г)
; г) 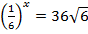 ;
;
д)  ; е)
; е)  ; ж)
; ж)  ; з)
; з) 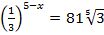 ;
;
и)  ; к)
; к) 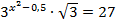 ; л)
; л) 
243. Решите уравнения:
а)  ; б)
; б)  ; в)
; в) 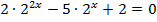 ;
;
г)  ; д)
; д) 
244. Решите уравнения:
а)  ; б)
; б)  ; в)
; в)  ;
;
г)  ; д)
; д) 
245. Решите неравенства:
а)  ; б)
; б)  ; в)
; в) 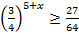 ; г)
; г) 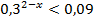 ;
;
д)  ; е)
; е)  ; ж)
; ж) 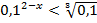 ; з)
; з)  ;
;
и) 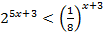 ; к)
; к)  ; л)
; л) 
246. Решите неравенства:
а)  ; б)
; б)  ; в)
; в)  ; г)
; г) 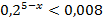 ;
;
д)  ; е)
; е)  ; ж)
; ж)  ; з)
; з)  ;
;
и)  ; к)
; к)  ; л)
; л) 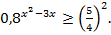
247. Решите уравнения:
а)  ; б)
; б)  ;
;
в)  ; г)
; г)  ;
;
д)  ; е)
; е)  ;
;
ж)  ; з)
; з)  ;
;
и) 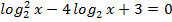 ; к)
; к)  .
.
248. Решите уравнения:
а) 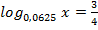 ; б)
; б)  ;
;
в)  ; г)
; г)  ;
;
д) 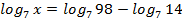 ; е)
; е)  ;
;
ж)  ; з)
; з)  ;
;
и)  ; к)
; к)  .
.
249. Решите неравенства:
а)  ; б)
; б)  ;
;
в)  ; г)
; г)  ;
;
д)  ; е)
; е)  ;
;
ж)  ; з)
; з)  ;
;
и)  ; к)
; к)  .
.
250. Решите неравенства:
а)  ; б)
; б)  ;
;
в)  ; г)
; г)  ;
;
д)  ; е)
; е)  ;
;
ж)  ; з)
; з)  ;
;
и)  ; к)
; к) 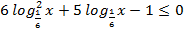 .
.
3 уровень
251. Решите уравнения:
а)  ; б)
; б)  ;
;
в)  ; г)
; г)  ;
;
д) 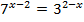 ; е)
; е)  ;
;
ж) 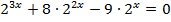 ; з)
; з) 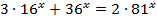 ;
;
и)  ; к)
; к)  ;
;
л)  ; м)
; м)  ;
;
н)  ; о)
; о)  .
.
252. Решите уравнения:
а)  ; б)
; б)  ;
;
в)  ; г)
; г)  ;
;
д)  ; е)
; е)  ;
;
ж)  ; з)
; з)  ;
;
и)  ; к)
; к)  ;
;
л)  ; м)
; м)  ;
;
н)  ; о)
; о)  .
.
253. Решите системы уравнений:
а)  ; б)
; б)  .
.
254. Решите системы уравнений:
а)  ; б)
; б)  .
.
255. Решите неравенства:
а)  ; б)
; б)  ;
;
в)  ; г)
; г)  ;
;
д)  ; е)
; е)  ;
;
ж)  ; з)
; з)  ;
;
и)  ; к)
; к)  ;
;
л)  ; м)
; м) 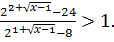
256. Решите неравенства:
а)  ; б)
; б)  ;
;
в)  ; г)
; г)  ;
;
д)  ; е)
; е)  ;
;
ж)  ; з)
; з)  ;
;
и)  ; к)
; к)  ;
;
л)  ; м)
; м) 
257. Решите систему неравенств:  .
.
258. Решите систему неравенств: 
259. Решите уравнения:
а)  ; б)
; б)  ;
;
в)  ; г)
; г)  ;
;
д)  ; е)
; е)  ;
;
ж)  ; з)
; з) 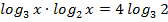 ;
;
и)  ; к)
; к) 
260. Решите уравнения:
а)  ; б)
; б)  ;
;
в)  ; г)
; г) 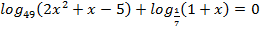 ;
;
д)  ; е)
; е) 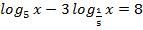 ;
;
ж)  ; з)
; з)  ;
;
и)  ; к)
; к) 
261. Решите неравенства:
а)  ; б)
; б)  ;
;
в)  ; г)
; г) 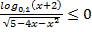 ;
;
д)  ; е)
; е)  ;
;
ж)  ; з)
; з)  ;
;
и)  ; к)
; к) 
262. Решите неравенства:
а)  ; б)
; б)  ;
;
в)  ; г)
; г)  ;
;
д)  ; е)
; е) 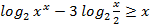 ;
;
ж)  ; з)
; з)  ;
;
и)  ; к)
; к) 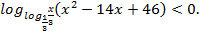
263. Решите системы уравнений и неравенств:
а)  ; б)
; б)  ;
;
в) 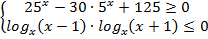 ; г)
; г)  .
.
264. Решите системы уравнений и неравенств:
а)  ; б)
; б)  ;
;
в)  ; г)
; г)  .
.
Date: 2015-10-18; view: 1057; Нарушение авторских прав