Основные операции над множествами

ПРЕДИСЛОВИЕ

На протяжении всей истории цивилизованного человечества математике придавалось особое значение, не случайно её считали и считают «царицей наук», и, как положено царице она и изящна, и красива, и величава, и труднодоступна.

В переводе с греческого μαθημα[матэма] – это знание, познание путём рассуждения. История науки и познания в целом убедительно подтверждают «непостижимую эффективность» математики, которая стала действенным, наиболее безупречным методом получения достоверного знания о мире.

Общепризнано, что математика является важнейшей составляющей человеческой культуры и её изучение во все времена и на всех ступенях образования считалось одним из приоритетных. Хорошее математическое образование и развитие математических способностей необходимо не только тому, кто впоследствии займётся научными исследованиями в области точных наук, но и тем, кто выберет для себя гуманитарное образование. Математический стиль мышления, умение рассуждать строго, без логических скачков, привычка к полноценности аргументации нужны также экономистам и историкам, биологам и лингвистам, психологам и юристам.

Данное пособие предназначено для студентов первого курса факультета непрерывного образования Российского Государственного Университета Правосудия, обучающихся по различным специальностям юридического и экономического профиля, но может быть использовано во всех учебных учреждениях среднего профессионального образования, где изучается общеобразовательная дисциплина «Математика», а также учащимися старших классов общеобразовательных школ, в том числе и для подготовки к ЕГЭ.

Содержание пособия в целом соответствует Примерной программе изучения математики в системе СПО. Незначительное отклонение в плане избыточности материала вызвано желанием представить некоторые разделы («Развитие понятия о числе», «Приложения определённого интеграла», «Элементы комбинаторики» и «Элементы теории вероятностей») в более полном, относительно законченном виде, а также дать возможность студентам, проявляющим интерес к математике, в какой-то мере удовлетворить его.

Предлагаемый к изучению материал представлен в пособии крупными блоками: алгебра, математический анализ, геометрия, стохастика (комбинаторика и теория вероятностей), что удобно для организации повторения и самостоятельной работы и позволяет «охватить» предмет в целом. Последовательность изучения тем, составляющих данные блоки, может быть различной, в соответствии с рабочими и календарно-тематическими планами той или иной специальности.

Учебное пособие в значительной мере представляет собой сборник задач, к большинству параграфов явно распределённых по уровням сложности, что позволяет учесть профиль специальности и адекватно организовать самостоятельную работу студентов, применяя индивидуальный подход. В то же время весь необходимый для выполнения заданий теоретический материал содержится в каждом параграфе и проиллюстрирован на конкретных разобранных примерах. Как правило, теоретический материал представлен кратко в виде перечисления основных формул и формулировок с соответствующими пояснениями и «картинками». Часть материала справочного характера (формулы планиметрии, таблицы квадратов, степеней, факториалов) размещена в приложении.

В пособии принята сквозная нумерация заданий, что на наш взгляд весьма удобно как для студентов, так и для преподавателей – позволяет облегчить указание и поиск заданий и ответов. Также для удобства пользования пособием в заданиях ко многим параграфам выдержан принцип парности, то есть задания в чётных номерах аналогичны заданиям в нечётных, что позволяет, например, решать нечётные номера в процессе занятий, а чётные – самостоятельно, для закрепления пройденного. Особенно это важно для слабоуспевающих студентов.

При подборе и составлении заданий были использованы различные источники (учебники, задачники и т.п.), авторам которых мы выражаем благодарность. Вся использованная литература указана в соответствующем списке на стр.226.

Считаем своим долгом выразить глубокую признательность рецензенту – кандидату физико-математических наук, доктору педагогических наук Е.И.Деза за ценные советы и пожелания, которые способствовали улучшению пособия, а также выразить благодарность Ю.М.Чернецовой за помощь в подготовке пособия к изданию.

Авторы.

Основные операции над множествами.

Обычно множества обозначаются заглавными буквами латинского алфавита: A, B, C … или перечислением (полным или частичным) его элементов, заключенных в фигурные скобки.

Примеры.

{1; 2; 3; 4; 5; 6; 7; 8; 9; 0} – множество цифр.

{1; 2; 3; 4; 5; 6; 7;…} – множество натуральных чисел.

Также множество можно записать, используя формулу, по которой вычисляются его элементы.

Пример. {2 n, n Î Z } – множество четных целых чисел.

(или {2 n | n Î Z } – множество всех чисел вида 2 n, где n – целое число).

Запись xÎ A означает, что x – элемент множества A. Символом Î обозначается отношение принадлежности. Запись x Ï A означает, что x не принадлежит A, то есть x не является элементом множества A.

Запись AÌ B означает, что множество A включается во множество B; множество A является подмножеством B, то есть все элементы множества A являются элементами множества B. Символом Ì обозначается отношение включения.

Определение. Пустым множеством называется множество, в котором нет ни одного элемента. Пустое множество обозначается символом Æ.

Определение. Множества A и B называются равными (A = B), если они состоят из одних и тех же элементов, или они оба пустые.

Определение. Объединением множеств A и B называется множество, состоящее из всех элементов, принадлежащих хотя бы одному из множеств A или B. A ∪ B = { x | xÎ A или xÎ B }	B A A ∪ B
Определение. Пересечением множеств A и B называется множество, состоящее из тех и только тех элементов, которые принадлежат и множеству A, и множеству B. A ∩ B = { x | xÎ A и xÎ B }	A ∩ B B A
Определение. Разностью множеств A и B называется множество, состоящее из тех множества A, которые не являются элементами множества B. A \ B = { x | xÎ A и x Ï B }	B A A \ B

Предполагается, что все встречающиеся в данном курсе множества являются подмножествами некоторого универсального множества U.

Определение. Дополнением множества A называется множество Ā = U \ A. Пример 1. = R \ Q. Множество иррациональных чисел является дополнением множества рациональных чисел Q до множества R действительных чисел.

Q R

Пример 2.

A = {1; 2; 3; 4; 5}; B = {1; 3; 5; 7; 9}.

A ∪ B = {1; 2; 3; 4; 5; 7; 9}; A ∩ B = {1; 3; 5}; A \ B = {2; 4}; A ∩Æ = Æ; A ∪ Æ = A;

A ∪ U = U; A ∩ U = A; U \ A = Ā.

Пример 3.

A = {1; 2; 3; 5; 7}; B = {2; 4; 6; 8}.

A ∪ B = {1; 2; 3; 4; 5; 6; 7; 8}; A ∩ B = Æ; A \ B = {1; 2; 3; 5; 7}.

Пример 4.

A = {1; 3}; B = {3}.

A ∪ B = {1; 3} = A; A ∩ B = {3} = B; A \ B = {1}.

Иногда удобно (для краткости) использовать следующие обозначения:

R \ {0} – все действительные числа, кроме нуля (R \ {0} = (– ∞; 0)∪(0; + ∞));

Z ⁺, Q ⁺, R ⁺ –положительные целые, рациональные, действительные числа, соответственно;

Z ^–, Q ^–, R ^– –отрицательные целые, рациональные, действительные числа, соответственно;

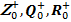–неотрицательные целые, рациональные, действительные числа, соответственно (то есть положительные и нуль);

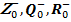–неположительные целые, рациональные, действительные числа, соответственно (то есть отрицательные и нуль).

Date: 2015-10-18; view: 685; Нарушение авторских прав