Факторгруппы

Пусть G – произвольная, не обязательно конечная группа.

Замечание. Так как " a, bÎ G (ab)(b ^-1a ^-1)= a(bb^-1)a ^-1 =

= aea ^-1 = e, то (ab) ^-1 = b ^-1a ^-1.

Теорема. Для подгруппы H Ì G эквивалентны следующие 4 условия:

1. " h Î H, " g Î G g ^-1hg Î H;

2. " g Î G g ^-1Hg Í H;

3. " g Î G g ^-1Hg = H;

4. " g Î G Hg = gH – то есть правые и левые смежные класы совпадают.

Доказательство. Очевидно, 1 Û 2 – это одно и то же условие, записанное в 1 для элементов, а в 2 для множеств. Также очевидно, что 3 Þ 2. Покажем, что 2 Þ 3. Заменим в условии 2 элемент g на g^-1. Получим gHg ^-1Í H. Умножим это включение слева на g ^-1 и справа на g. Получим HÍ g^-1Hg. Это включение вместе с включением из 2 дает равенство 3. Следовательно, 2 Û 3. И наконец, равенство 4 получается умножением равенства 3 на g слева, а равенство 3 получает-

ся умножением равенства 4 на g ^-1 справа. То есть 3 Û 4.

Определение. Подгруппа H Ì G называется нормальной

подгруппой (или нормальным делителем) в G, если для Н выполняется любое из четырёх эквивалентных условий теоремы (а, следовательно, и все четыре условия).

Очевидно, в коммутативной группе любая подгруппа – нормальная.

В случае нормальной подгруппы Н фактормножество G/~

мы будем обозначать G / H. В этом случае левые и правые смежные классы совпадают, и их можно просто называть смежными классами. Обозначать смежный класс элемента g мы будем .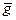

Очевидно, тривиальные подгруппы {e} и G – нормальны.

Пусть Н – нормальная подгруппа в G. Зададим на фактормножестве G / H структуру группы.

I. Пусть для 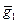, 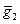Î G/H по определению × = .

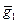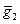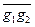Утверждение. Определение умножения на G/H коррект-

но, то есть не зависит от выбора представителей в классах 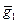и .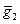

Доказательство. Пусть g₁¢Î 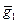, g₂¢Î 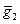- другие представители в классах. Покажем, что g₁¢g₂¢ Î 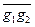, то есть g₁¢g₂¢ ~ g₁g₂. В самом деле, g₁¢ ~ g₁ , g₂¢ ~ g₂ Þ g₁¢ = h₁g₁, g₂¢= h₂g₂ Þ g₁¢g₂¢= h₁g₁h₂g₂=h₁g₁h₂(g₁^-1g₁)g₂= h₁(g₁h₂g₁^-1)g₁g₂= = h₁h¢g₁g₂ = h¢¢g₁g₂, и h¢¢Î H Þ g₁¢g₂¢ ~ g₁g₂, = .



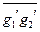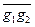II. Проверим свойства из определения группы.

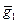
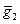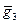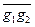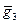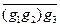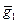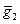
1. ( ) = × = = = ( 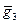) – ассоциативность в G / H выполняется.

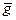
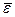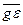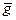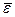
2. = = = 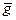, то есть в G / H $ нейтральный элемент .

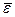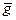
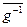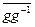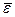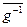
3. Очевидно, = = = 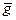, то есть в G / H

для элемента 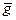$ обратный элемент 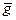^-1 = .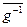

Таким образом, на фактормножестве G / H мы задали

структуру группы, которая называется факторгруппой.

Date: 2015-09-25; view: 302; Нарушение авторских прав