Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Нормальный вид эрмитовых форм
|
|
Пусть f(x, y) – эрмитова форма на линейном пространстве L над полем С, F(x) – соответствующая квадратичная форма.
Теорема. В L существует f- ортогональный базис.
Доказательство аналогично доказательству из п.24.6.
Пусть e¢ = {е1,…,еn} - f- ортогональный базис, и пусть f(еk, еk) = lk "k. Тогда в этом базисе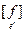 
= diag(l1,…,ln), где все lk Î R, f(x, y) = 
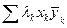, F(x) = 
, и такой вид эрмитовых форм f и F называется каноническим. Следовательно, любая эрмитова полуторалинейная форма и любая эрмитова квадратичная форма эквивалентны формам канонического вида. То есть существует линейная замена координат, которая приводит произвольную эрмитову полуторалинейную форму (квадратичную форму) к каноническому виду.
Пусть f(еk, еk) = lk ¹ 0 при k =1,…,r и f(еk, еk)= 0 при
k = r+1,…,п. Тогда r = rg f = rgF, и r от базиса не зависит.
Будем считать теперь, что форма F имеет канонический вид F(x) = l1 | х1 | 2+…+ls | xs | 2 – ls+1 | хs+1 | 2–…–ls+t | хs+t | 2, где все lk > 0, s + t = r. Пусть mk = 
при k = 1,…,r, mk = 1 при k = r+1,…,п. Тогда после замены координат zk = mkxk " k получим F(x)= | z1 | 2+…+ | zs | 2– | zs+1 | 2-…- | zs+t | 2 - такой вид квадратичной формы называется нормальным.
Таким образом, имеет место
Теорема. В линейном пространстве L над полем С для
любой эрмитовой формы F существует базис, в котором форма имеет нормальный вид F(z) = z12+…+zs2– zs+12-…-zs+t2. Соответствующая эрмитова полуторалинейная форма f имеет нормальный вид f(z, w) = z1w1+…+zsws – zs+1ws+1-…- zs+tws+t.
Как и в п.24.6 для эрмитовых форм F можно дать определения положительно определённой или положительной формы (F > 0), отрицательно определённой или отрицательной формы (F < 0), неотрицательно определённой формы (F ³ 0), неположительно определённой формы (F £ 0), неопределённой формы. Во всех этих случаях условия на s и t будут такие же, как и в п.24.6.
По аналогии с п.24.7 для эрмитовых форм формулируется и доказывается закон инерции, определяется положительный индекс инерции формы I+(F)= s и отрицательный индекс инерции формы I -(F) = t.
Так же эрмитовы квадратичные формы имеют 2 числовых инварианта I+ = s, I - = t, которые независимы и составляют полную систему инвариантов.
Аналогично как и в п.24.8 формулируется и доказывается критерий Сильвестра. Необходимо лишь заметить, что угловые подматрицы эрмитовой матрицы являются эрмитовыми, а определители эрмитовых матриц Мk Î R.
Лекция 38.
Date: 2015-09-25; view: 398; Нарушение авторских прав