Приведение эрмитовой формы унитарным преобразованием координат

Теория эрмитовых форм в унитарном пространстве аналогична теории квадратичных форм в евклидовом пространстве (см. п.25).

Пусть Н^п унитарное пространство с ортонормированным базисом и, F(x) – эрмитова квадратичная форма с матрицей 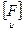в базисе и и f(x,у) – соответствующая эрмитова полуторалинейная форма с матрицей = 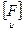. Рассмотрим линейный оператор j с матрицей = 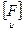. Так как матрица 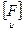- эрмитова, то j - эрмитов оператор, j* = j. По теореме о структуре эрмитова оператора в Н^п существует ортонормированный базис и¢, в котором матрица оператора j диагональна: = diag(l₁,l₂,…,l_n), причем все l_iÎ R. Пусть

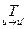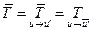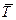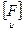Т = . Тогда Т – унитарная матрица (так как по столбцам матрицы Т стоят координаты векторов из ортонормированного базиса и¢), и, значит, Т ^-1= . Но . Пусть Т₁= . Тогда = diag(l₁,l₂,…,l_n) = Т ^-1 Т = Т =

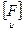
= = - диагональная матрица, причем 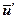- ортонормированный базис. Следовательно, если в базисе 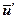вектор у имеет координаты (y₁,…,y_n), то форма F имеет канонический вид F(у)=l₁ | y₁ | ²+l₂ | y₂ | ²+…+l_n | y_n | ², причем все l_iÎ R. Соответственно, если в этом базисе вектор z = (z₁,…,z_n), то f(y, z) = l₁y₁ 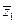+ l₂y₂ 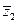+ …+ l_ny_n 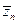. Таким образом, нами

доказана

Теорема. Для любой эрмитовой квадратичной формы F(x) в унитарном пространстве Н^п существует ортонормированный базис 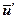, в котором форма F имеет канонический вид F(у) = l₁ | y₁ | ²+ l₂ | y₂ | ²+…+ l_n | y_n | ², причем все l_iÎ R. Это означает, что существует унитарная матрица Т₁ перехода к новому базису 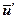, в котором матрица формы F диагональна:

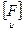
= = diag(l₁,l₁,…,l_n), причем все l_iÎ R.

Следствие 1. Эрмитовы формы F и f унитарно эквивалентны формам, имеющим канонический вид (см. п.24.5).

Следствие 2. Две эрмитовы квадратичные формы канонического вида унитарно эквивалентны тогда и только тогда, когда их коэффициенты l₁,l₂,…,l_n отличаются, может быть, лишь порядком.

Следствие 3. Две эрмитовы квадратичные формы унитарно эквивалентны тогда и только тогда, когда их матрицы даже в различных ортонормированных базисах имеют одинаковые характеристические многочлены.

Так как коэффициенты l₁,…,l_n формы F – это собственные значения линейного оператора j, то найти их можно, решая характеристическое уравнение для матрицы = ,

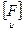то есть уравнение det( 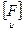-lE) = 0. Векторы базиса

и¢ = {и¢₁,…, и¢_n} – это собственные векторы линейного оператора j, и найти все и¢_i можно, решая однородные системы линейных уравнений ( 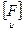- l _iE) [ x ] = [ 0 ]. Различным собственным значениям соответствуют ортогональные друг другу собственные векторы, и, если dim Ker( 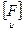- l _iE) = 1, то найденный вектор необходимо лишь нормировать, то есть разделить на его длину. Если же имеются одинаковые собственные значения, то есть кратные корни l_i характеристического уравнения, то dim Ker( 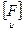- l _iE)> 1, и найденную фундаментальную систему решений для СЛУ ( 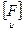- l _iE) [ x ] = [ 0 ] необходимо ортонормировать, например, по Граму-Шмидту. Затем, после нахождения базиса и¢ надо перейти к базису 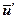, заменив все векторы и¢₁,…, и¢_n на «комплексно сопряженные».

Date: 2015-09-25; view: 477; Нарушение авторских прав