
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Замечания. 1. Функции, для которых выполнены условия 1, 2 из определения и 1, 2 из следствия называются полуторалинейными (они линейны по первому аргументу и полулинейны
|
|
1. Функции, для которых выполнены условия 1, 2 из определения и 1, 2 из следствия называются полуторалинейными (они линейны по первому аргументу и полулинейны по второму). Таким образом, любая эрмитова функция - полуторалинейная.
2. Теория эрмитовых функций аналогична теории симметричных билинейных функций, поэтому многие утверждения будут лишь сформулированы, а их доказательства читателю предлагается провести в качестве упражнений.
Примером эрмитовой функции служит скалярное произведение на унитарном пространстве.
Пусть f - полуторалинейная функция на n -мерном пространстве L = Ln над полем С, e = {e1, …,en} – произвольный
базис в L. Если x, yÎ L,  где все
где все
xs, ytÎ С, то f(x,y) = 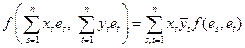 . Из
. Из
этой формулы видно, что значение полуторалинейной функции f(x, y) при произвольных x, yÎ L полностью и однозначно определяется n2 значениями fst = f(es,et) функции f на упорядоченных парах базисных векторов es, et.
Матрицу [ 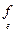 ] =(fst)s,t=1,…,n будем называть матрицей полуторалинейной функции f в базисе e.
] =(fst)s,t=1,…,n будем называть матрицей полуторалинейной функции f в базисе e.
Пусть  . Тогда f(x,y)=
. Тогда f(x,y)= 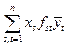 =
=  , то есть функция f(x, y) является многочленом, все одночлены которого – первой степени от координат вектора х и первой степени от координат вектора
, то есть функция f(x, y) является многочленом, все одночлены которого – первой степени от координат вектора х и первой степени от координат вектора  . Такой многочлен является линейной формой по х и полулинейной по у, то есть полуторалинейной формой. Полуторалинейные формы, соответствующие эрмитовым функциям, будем называть эрмитовыми формами. Необходимым и достаточным условием эрмитовости полуторалинейной формы f явлется условие fts = f(et,es)=
. Такой многочлен является линейной формой по х и полулинейной по у, то есть полуторалинейной формой. Полуторалинейные формы, соответствующие эрмитовым функциям, будем называть эрмитовыми формами. Необходимым и достаточным условием эрмитовости полуторалинейной формы f явлется условие fts = f(et,es)=  =
= 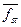 " s,t, то есть [
" s,t, то есть [ 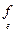 ] t=
] t= 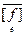 в любом (в некотором) базисе е – это условие эрмитовости её матрицы [
в любом (в некотором) базисе е – это условие эрмитовости её матрицы [ 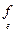 ] в любом (в некотором) базисе е.
] в любом (в некотором) базисе е.
Определение. Пусть f - полуторалинейная функция на линейном пространстве L над С. Функция F: L ® С, заданная формулой F(x) = f(x, x) " x Î L, называется квадратичной функцией, определяемой полуторалинейной функцией f. Если f – эрмитова, то и F называется эрмитовой.
Очевидно, если f(x, y) = 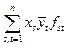 , то F(x) =
, то F(x) = 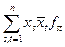 -
-
форма второй степени от действительных и мнимых частей
координат х.
Матрицей квадратичной формы F будем называть матрицу соответствующей полуторалинейной формы f: [  ] = [
] = [ 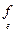 ]. И тогда F(x) =
]. И тогда F(x) =  .
.
Упражнение. Проверить, что полуторалинейная форма f однозначно восстанавливается из определенной ею квадратичной формы F по формуле
f(x, y)= 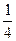 (F(x+y) - F(x - y) + iF(x+iy) - iF(x - iy)). (26.1)
(F(x+y) - F(x - y) + iF(x+iy) - iF(x - iy)). (26.1)
Если e ¢ = {e¢1,…,e¢n} - другой базис в L, и Т = 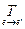 = (tks) - матрица перехода от базиса e к базису e ¢, то
= (tks) - матрица перехода от базиса e к базису e ¢, то
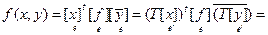
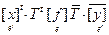 . Сле-
. Сле-
довательно,  , или
, или 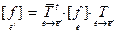 , где
, где  - матрица перехода от базиса e к «комплексно сопряженному» с e¢ базису
- матрица перехода от базиса e к «комплексно сопряженному» с e¢ базису 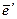 , состоящему из векторов
, состоящему из векторов
 , s=1,…,n. Аналогично,
, s=1,…,n. Аналогично, 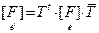 .
.
Date: 2015-09-25; view: 461; Нарушение авторских прав