Следствия. 2. Если det Î R, то sign(det )= sign(det )

1. det = det 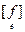×| detT|².

2. Если det 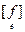Î R, то sign(det 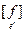)= sign(det ).

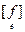Определение. Пусть f - полуторалинейная форма на L. Рангом формы f называется ранг ее матрицы в каком-либо базисе: rg f = rg 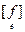. Аналогично, rg F = rg 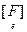= rg f.

Корректность определения следует из того, что rg 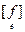от базиса e не зависит.

Теорема. Полуторалинейная форма f является эрмитовой тогда и только тогда, когда соответствующая f квадратичная форма F принимает на L только действительные

значения, то есть " xÎ L F(x) = f(x, x) Î R.

Доказательство. Если f - эрмитова форма, то " x, y Î L f(x,y)= 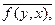поэтому " xÎ L F(x)=f(x,x)= 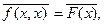так что F(x) Î R " xÎ L.

Наоборот, пусть теперь " xÎ L F(x) = f(x, x) Î R. Покажем, что тогда " x, yÎL f(x, y)= 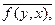то есть f – эрмитова. Используем формулу (26.1): " x, y Î L

f(x, y) = 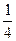(F(x + y) – F(x - y)+ iF(x + iy) – iF(x - iy)),

причем "x, y Î L F(x+y)= F(y+x)Î R,

F(x - y)= f(x - y, x - y)= (-1)²f(y - x, y - x)= F(y – x)Î R,

F(x + iy)= i× 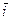×f(x + iy, x + iy)= f(- y+ ix,- y+ ix)=

= (-1)²f(y - ix, y - ix)= F(y – ix)Î R, и аналогично

F(x - iy)= F(y + ix)Î R.

Подставив последние четыре формулы в (26.1), получим:

f(x, y)= 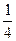(F(y+ x) - F(y – x) + i F(y – ix) - i F(y + ix))= .

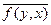Следовательно, f - эрмитова форма.

ÿ

Date: 2015-09-25; view: 325; Нарушение авторских прав