Обратная матрица

Утверждение. Пусть А - (т,п)- матрица, В - (п,k)- матрица. Тогда (АВ) ^t = В ^tА ^t.

Доказательство. Заметим, что произведение В^tА^t определено, так как В ^t - (k,п)- матрица, а А ^t - (п,т)- матрица. Кроме того (АВ) ^t и В ^tА ^t – матрицы одного типа.

Очевидно, (i,j)- й элемент матрицы (АВ)^t равен ((АВ)^t)_i,j= =(АВ)_j,i = А_j×Вⁱ = (j-я строка матрицы А)×(i-й столбец матрицы В) = (В ^t)_i×(А ^t)^j = (i-я строка матрицы В ^t)×(j-й столбец матрицы А ^t) = (В ^tА ^t)_i,j.

ÿ

В 8.4 мы доказали, что если левая и правая обратные матрицы для (п,п)- матрицы А существуют, то они совпадают.

Теорема. А^-1 $ Û |A| ¹ 0.

Доказательство. Þ. Пусть А^-1= В $. Тогда АВ = Е Þ | АВ| = | А||В| = |E| = 1 Þ |A| ¹ 0.

Ü. Пусть |A| ¹ 0. Найдем правую обратную матрицу Х такую, что АХ = Е. Столбцы матрицы Х обозначим Х¹, Х²,…,Х^п, а столбцы матрицы Е обозначим Е¹, Е²,…,Е^п. Тогда из уравнения АХ = Е, записывая матрицы X и E через столбцы, получим уравнение А×(Х¹, Х²,…,Х^п) = (Е¹, Е²,…,Е^п), или

(А×Х¹, А×Х²,…, А×Х^п) = (Е¹, Е²,…,Е^п) Þ А×Х ⁱ = Е ⁱ " i. Так как |A| ¹ 0, то по правилу Крамера решение Х ⁱ " i существует и единственно. Таким образом, доказано, что правая обратная матрица для А существует и единственна. Аналогично можно доказывать существование левой обратной матрицы. Но можно поступить иначе. Так как |A ^t| = |A| ¹ 0, то для A^t по доказанному существует правая обратная матрица Y, то есть A^tY = Е Þ (A^tY) ^t = Е ^t= Е Þ Y ^tA^tt= Е Þ Y ^tA= Е Þ Y ^t – левая обратная матрица для А.

ÿ

Далее мы найдем, какой вид имеет обратная матрица.

Рассмотрим уравнение для i- го столбца обратной матрицы А×Х ⁱ = Е ⁱ из доказательства предыдущей теоремы. Так как Е ⁱ= 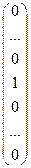- здесь 1 находится на i- м месте, Х ⁱ = 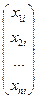, то по правилу Крамера х_ki = D_k / |A|, k = 1,…,п, где D_k - определитель, полученный из определителя |A| заменой k- го столбца на Еⁱ. Из разложения D_k по k- му столбцу получим, что D_k=А_ik – алгебраическое дополнение к (i,k)- му элементу в |A|. Значит, х_ki = А_ik/|A|, i, k = 1,…,п. Матрица А* = (a_ki), где

a_ki = А_ik, называется присоединенной матрицей к А. Таким образом, нами доказана

Теорема. Если |A| ¹ 0, то А^-1 $, и А^-1=(1/|A|)×А*.

Упражнение. Проверить, что А×А*=А*× А = |A|×E при любом |A|.

Date: 2015-09-25; view: 330; Нарушение авторских прав