Следствия. 5. Целые кратные элементов кольца

1) Так как -(- х)= х, то (-a)(-b) = - (a(-b)) = - (- (ab) = ab.

2) Если K ' 1, то a(- 1) = (- 1)a = - (1× a) = - a.

5. Целые кратные элементов кольца.

Пусть по определению "nÎZ na= 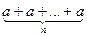при nÎN,

na = 0_K, при n = 0, na = - ((-n)a) при - nÎN.

Упражнения.

1) Доказать, что "nÎZ -(na) = (-n)a = n(- a).

2) Доказать, что "m,nÎZ, " a, b Î K n(a+b)=na +nb,

(m+n)a = ma+na.

3) Доказать, что "m, nÎZ, " aÎ K m(na)=(mn)a.

4) Доказать, что "nÎZ, " a, b Î K n(ab)=(na)b = a(nb).

5) Доказать, что "m,nÎZ, " a, b Î K (ma)(nb)=(mn)(ab).

6) Доказать, что если K ' 1_K, то na = (n 1_K)a.

Замечание. Если "nÎZ, " aÎ K определить операцию

n×a = na, то свойства из упражнений 2), 3), 4), 6) означают, что кольцо K является унитарной алгеброй над Z.

6. В АКУ-кольце " a, b Î K " nÎN справедлива фор­мула бинома Ньютона (а + b)ⁿ = .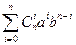

Определение. Подмножество K₁Í K называется под­кольцом в K, если K₁ само является кольцом относительно операций K.

Очевидно, в любом кольце K всегда существуют триви­альные подкольца K и {0}.

6.3. Делители нуля.

Определение. Если кольцо K' a, b такие, что ab = 0, но

a ¹ 0, b ¹ 0, то a называется левым делителем нуля, а b –

правым делителем нуля. Элемент кольца называется делите­лем нуля, если он является одновременно левым и правым делителем нуля. Если a - делитель нуля, то пишут: a | 0.

Очевидно, в коммутативном кольце множества делите­лей нуля, левых делителей нуля и правых делителей нуля совпадают.

Аналогично, в коммутативном кольце мы будем писать a | с, если $ b Î K такой, что ab = c.

Если a | 1, то а – обратимый элемент кольца.

Если K – поле, то " aÎ K, a ¹ 0, из определения поля a |1.

Date: 2015-09-25; view: 402; Нарушение авторских прав