Доказательство

p - рефлексивно, так как " аÎ Z a – a = 0×m Þ a p a.

p - симметрично, так как если a p b, то a – b = km, kÎ Z Þ

b – a =(-k)m, и -kÎ Z Þ bp a.

p - транзитивно, так как если a p b, и bp с, то a – b = km, где kÎ Z, b – c = lm, где lÎ Z Þ (a – b) +(b – c) = a – c = (k+l)m, и k+lÎ Z Þ a p с.

ÿ

Классы эквивалентных элементов по отношению p мы будем обозначать cl_p a или (если ясно, какое p имеется ввиду) cl a или 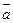. Очевидно, cl_p a = {b Î Z | bp a } =

= { b Î Z | b – a = km для некоторого k Î Z }=

= { b Î Z | b – a Î m Z } = { b Î Z | b Î a + m Z } = a + m Z.

Так как p - отношение эквивалентности на Z, то Z разбива­ется на непересекающиеся классы эквивалентных элементов.

Фактормножество Z/ p, то есть множество классов эквива­лентных элементов, мы будем обозначать Z_m или Z/ (m).

Если bÎ cl a, то говорят, что b – представитель из cl a.

Очевидно, при m = 0 " a cl a = a, а отношение эквивалентности – это отношение равенства. Таким образом, при m = 0 Z_m = Z.

Далее будем считать, что m ¹ 0.

Если a p b, то часто пишут a 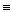b(mod m) или a 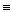b(m), и говорят, что a и b сравнимы по модулю m. А классы эквива­лентных элементов называют классами вычетов по модулю m или классами по модулю m.

Разделим a и b на m с остатком. Пусть a = mq₁ + r₁,

b = mq₂ + r₂, где 0 £ r₁< m, 0 £ r₂< m. Очевидно, a - r₁= mq₁,

то есть m|(a – r₁) Þ 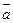= 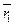. Аналогично, = .

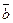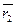Утверждение. 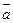= 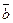Û r₁= r₂.

Доказательство. Ü. Пусть r₁= r₂. Тогда = = = .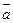

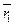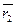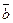Þ. Пусть 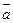= 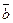, и r₁ ¹ r₂, например, r₁ >r₂. Тогда = = =

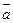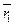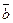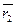
Þ r₁p r₂ Þ m| (r₁ - r₂). Но 0 < r₁ - r₂ < m. Получили противо­речие, то есть r₁= r₂.

ÿ

Из утверждения мы получаем, что различных классов по модулю m ровно столько, сколько существует различных ос­татков от деления на m, то есть существует m различных классов, и Z_m = { , , ,…, }.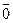

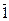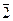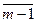Очевидно, = , = , = , = .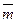

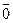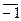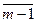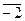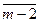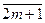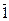Зададим на Z_m структуру кольца.

I.Определим операции сложения и умножения так:

пусть + = , × = .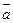

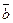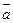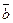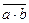Докажем корректность нашего определения, то есть неза­висимость его от выбора представителей в классах.

Пусть a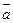₁Î , b₁Î 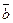, то есть = 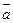, = 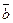. Тогда

a₁= a + km, b₁= b + lm, и a₁+ b₁= a + b + (k + l)m,

a₁ b₁= ab +(kb + al + klm)m Þ (a₁+ b₁)p (a + b), (a₁ b₁)p(a b) Þ 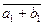= , 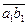= . Корректность доказана.

II. Проверим свойства операций.

1. ( + )+ = + = = = + =

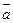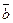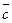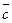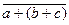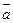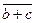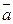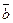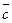= +( + ) – это свойство ассоциативности сложения в Z_m следует из ассоциативности сложения в Z.

2. Так как " 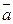Î Z_m 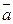+ = 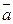, то в Z_m $ нейтральный

элемент по сложению.

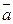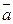3. Так как " Î Z_m + = , то " 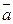Î Z_m $ проти­воположный элемент по сложению: - = .

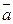Свойства 4, 5, 8, 9 из определения кольца следуют из соот­ветствующих свойств кольца целых чисел и доказываются так же, как и свойство 1.

Упражнение. Доказать свойства 4, 5, 8, 9.

6. Так как " 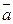Î Z_m 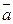× 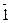= 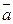, то в Z_m $ нейтральный

элемент по умножению.

Таким образом, мы доказали, что Z_m - АКУ-кольцо.

Пример. Выпишем таблицы сложения и умножения для Z₆.

Таблица сложения

Таблица умножения

+

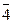
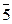
х

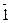
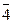
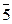
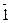
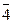
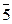
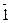
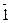
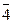
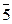
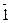
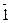
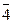
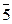
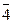
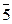
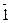
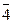
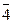
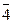
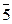
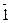
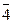
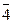
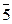
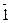
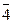
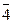
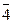
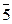
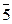
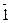
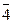
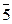
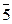
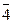
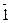
Так как × = , то и в Z₆ являются делителями нуля. В то же время 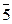× 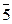= 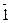, то есть 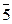- обратимый элемент в Z₆.

Утверждение. Элемент 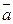Î Z_m обратим Û НОД(a,m)= 1.

Date: 2015-09-25; view: 358; Нарушение авторских прав