
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Доказательство. Þ. Пусть $ Î Zm такой, что = Û (ab)p 1Û ab = 1 + km
|
|
Þ. Пусть $ 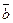 Î Zm такой, что
Î Zm такой, что 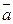
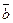 =
= 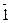 Û (ab)p 1Û ab = 1 + km
Û (ab)p 1Û ab = 1 + km
Û ab - km = 1, и если d|a, d|m, то d|1.
Ü. Пусть НОД(a,m) = 1. Тогда " 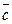 ,
, 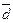 Î Zm,
Î Zm, 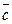 ¹
¹ 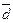 , также
, также 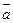
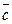 ¹
¹ 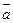
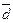 . В самом деле, если
. В самом деле, если 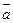
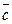 =
= 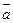
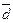 , то
, то  =
= 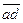 Þ (ac)p(ad) Þ m|(ac - ad) Þ m|a(c - d). Но НОД(a,m) = 1Þ
Þ (ac)p(ad) Þ m|(ac - ad) Þ m|a(c - d). Но НОД(a,m) = 1Þ
m|(c - d) Þ cp d Þ 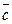 =
= 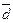 - противоречие. Таким образом, все
- противоречие. Таким образом, все
элементы из 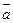 × Zm различны Þ
× Zm различны Þ 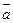 × Zm = Zm Þ $
× Zm = Zm Þ $ 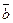 Î Zm
Î Zm
такой, что 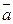
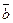 =
= 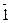 .
.
ÿ
Следствие. Zm – поле Û m – простое число.
Доказательство. Ü. Если m = p – простое число, то
" a Î {1,2, …, p - 1} НОД(a,p)= 1 Þ 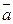 - обратим, Zm – поле.
- обратим, Zm – поле.
Þ. Пусть Zm – поле, и m – непростое число, m = kl, где k > 1, l > 1. Тогда НОД(k, m) ¹ 1, и для элемента 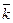 Î Zm,
Î Zm, 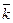 ¹
¹ 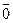 , обратный элемент в Zm не существует - противоречие. Значит, m – простое.
, обратный элемент в Zm не существует - противоречие. Значит, m – простое.
ÿ
Поля.
Примеры числовых полей хорошо известны – это
< Q ,+, ×, -(), 0, 1 >, < R ,+, ×, -(), 0, 1 >, < C ,+, ×, -(), 0, 1 >.
Также мы доказали, что " простого числа p Î Z полем является < Zp ,+, ×, -(), 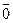 ,
, 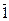 >.
>.
Определение. Если P = <P, +, ×, -(), 0K, 1K > - поле,
FÍ P и F = <F,+, ×, -(), 0K, 1K > - поле, то F называют подполем поля P, а P называют надполем поля F или расширением поля F. Если ясно, какие операции имеются в виду, то говорят, что F – подполе поля P, а P – расширение поля F.
Определение. Если Р1, Р2 – поля, то отображение
j: Р1® Р2 называется изоморфизмом полей, если j - биекция, и " x,yÎ Р1 j(x+y) = j x +j y, j(x×y) = j x ×j y. Если для полей Р1 и Р2 такой изоморфизм существует, то говорят, что поля Р1 и Р2 изоморфны и пишут Р1» Р2.
Date: 2015-09-25; view: 507; Нарушение авторских прав