Примеры колец

1. < Z,+, ×> - АКУ-кольцо целых чисел.

2. < 2Z,+, ×> - неунитарное АК-кольцо чётных чисел.

3. < nZ,+, ×> - неунитарное АК-кольцо чисел, кратных n,

где nÎZ, n ¹ ±1.

4. R [ x ] - АКУ-кольцо многочленов с действительными

коэффициентами.

5. С [ a,b ] - АКУ-кольцо функций, непрерывных на

от­резке [ a,b ].

6. <0_K,+,×> - тривиальное АКУ-кольцо, в котором 1_K = 0_K.

7. Пусть K₁ и K₂ – кольца. Рассмотрим множество

K₁ ´ K₂ = {(a,b)| aÎ K₁, bÎ K₂}. Пусть по определению

(a₁,b₁)+ (a₂,b₂) = (a₁+a₂, b₁+b₂), (a₁,b₁)(a₂,b₂) = (a₁a₂, b₁b₂). Тогда K₁ ´ K₂ – кольцо, причем, если K₁, K₂ - АКУ-кольца, то K₁ ´ K₂ – АКУ-кольцо.

Упражнение. Проверить, что универсальные алгебры в

примерах 1 – 7 являются кольцами.

6.2. Простейшие свойства колец.

1. " a Î K a×0 = 0× a = 0.

Доказательство. 0 + 0 = 0 Þ a×(0 + 0) = a×0 Þ

a×0 + a×0= a×0 Þ -(a×0)+ (a×0 + a×0)= -(a×0)+ a×0Þ

(-(a×0)+ a×0) + a×0= 0 Þ 0 + a×0 = 0 Þ a×0 = 0.

Аналогично, 0× a = 0.

2. Если 1 = 0, то K = {0} – тривиальное кольцо.

Доказательство. " a Î K a = 1× a = 0× a = 0.

3. Общий закон дистрибутивности: " m ³ 1, n ³ 1

()×()= .

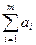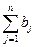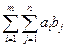Доказательство индукцией по s = m + n.

При m = n = 1 утверждение очевидно: a₁b₁ = a₁b₁.

Пусть m ³ 2 или n ³ 2 и пусть для s = m + n – 1 утвержде­ние верно. Тогда (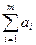)×()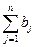=( 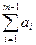+a_m)×( 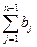+b_n)=

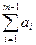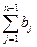=()×( +b_n)+a_m( 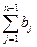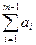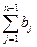+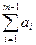b_n)=()()+()b_n +

+ a_m×(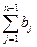)+ a_m× b_n = .

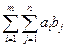4. Правило знаков. " a, b Î K (- a)b = a(- b) = - (ab).

Доказательство. 0=a(b+(– b))=ab+ a(- b) Þ a(- b)=- (ab).

Аналогично, (- a)b = - (ab).

Date: 2015-09-25; view: 358; Нарушение авторских прав