Упражнения. 1. Доказать, что id: Р1® Р1 является изоморфизмом, то есть Р1 » Р1

1. Доказать, что id: Р₁® Р₁ является изоморфизмом, то есть Р₁» Р₁.

2. Доказать, что если j:Р₁®Р₂ – изоморфизм, то j ^-1:Р₁®Р₂ – изоморфизм, то есть если Р₁» Р₂, то Р₂» Р₁.

3. Доказать, что если j:Р₁® Р₂, y:Р₂® Р₃ – изоморфизмы,

то y ◦j:Р₁® Р₃ – изоморфизм, то есть если Р₁» Р₂ и Р₂» Р₃, то Р₁» Р₃.

4. Доказать, что если j:Р₁® Р₂ – изоморфизм, то

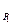j(0 )=j(0 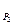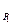), j(1 )=j(1 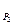),j(-х)= - jх "хÎР₁,

j(х ^-1)= (j х)^-1 "хÎ Р₁, х ¹ 0 .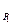

Пусть P - поле. Будем обозначать элементы вида

ab^-1 = b^-1a дробями . Тогда = 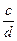Û ab^-1 = cd ^-1Û

ad = bc, + 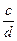= ab^-1+cd ^-1 =(ab^-1+cd ^-1)×bd×(bd) ^-1 =

= (ad + bc)(bd) ^-1= 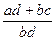, × 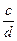= ab^-1×cd ^-1 =ac(bd) ^-1= .

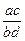Любое поле P содержит элементы 0_Р, 1_Р, 1_Р + 1_Р = 2(1_Р), 1_Р + 1_Р +1_Р =3(1_Р),…, m(1_Р) "m Î N. Возможны два случая:

1) все элементы вида m(1_Р), m Î N, различны.

2) среди этих элементов $ одинаковые, то есть в N $ m ¹ n: m(1_Р)= n(1_Р) (такой случай имеет место всегда для конечного поля Р). Пусть m > n. Тогда (m – n)(1_Р)= 0_Р , то есть существует такое t Î N, что t(1_Р)= 0_Р .

Определение. Характеристикой поля Р называется наименьшее натуральное число t такое, что t(1_Р)= 0_Р . Если такого числа не существует (как в случае 1), то говорят, что характеристика поля равна 0 или ∞. Характеристика поля обозначается через char P.

Очевидно, char Q = char R = char C = 0, char Z_p = p.

Теорема. Если р = char P ¹ 0, то р – простое число.

Доказательство. Пусть р – не простое, p = kl, где k, l ¹ 1.

Тогда 0_Р = p(1_Р)= (kl)(1_Р) = k(1_Р)× l(1_Р), и k(1_Р) ¹ 0_Р, l(1_Р) ¹ 0_Р. Но в поле нет делителей нуля (см. 6.3), то есть мы получили противоречие. Значит, р – простое число.

ÿ

Определение. Поле Р называется простым, если у него нет подполей, отличных от Р.

Теорема. Поле Q – простое.

Доказательство. Пусть Q Ê Р – подполе. Тогда Р ' 0, 1, 1+1=2, 2+1=3,…, n ("n Î N ), - n ("n Î N ), ± 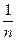("n Î N ), 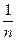×m ("n Î N, m Î Z ), то есть Р Ê Q Þ Р = Q. Других подполей в Q нет.

ÿ

Теорема. Поле Z_p – простое.

Доказательство. Пусть Z_p Ê Р – подполе. Тогда Р 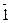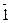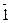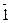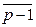' , , + = , + = , …, , то есть Р Ê Z_p Þ Р = Z_p. Других подполей в Z_p нет.

ÿ

Теорема. Пусть Р – поле, и char P = 0. Тогда

1) P содержит наименьшее (по включению) подполе Р₀,

2) подполе Р₀ – простое,

3) Р₀» Q.

Доказательство. Очевидно, пересечение всех подполей в Р является, во-первых, подполем, во-вторых, оно является наименьшим подполем (так как содержится в любом другом) и, в-третьих, оно является простым подполем, так как не содержит собственных (меньших) подполей. Отсюда следуют 1-е и 2-е утверждения теоремы.

Но мы докажем теорему иначе. Пусть поле P содержит под­поле Р₁. Тогда Р₁ ' 0_Р, 1_Р, 1_Р+1_Р=2(1_Р), 2(1_Р)+1_Р =3(1_Р),…, n(1_Р) ("n Î N ), (- n)(1_Р) ("n Î N ), ±(n(1_Р))^{- 1} ("n Î N ), m(1_Р)×(n(1_Р))^{- 1} ("n Î N, m Î Z ). Пусть

Р₀={m(1_Р)×(n(1_Р))^{- 1}| nÎ N, mÎ Z }= { 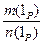| mÎ Z, nÎ N }. Тог­да Р₀ - подполе, так как

I. 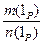+ = 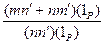Î Р₀ (*)

и 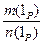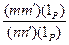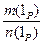= Î Р₀ " , Î Р₀ , (**)

II.2. при m = 0, n = 1 получаем, что 0_P Î Р₀ ,

3. - 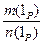= 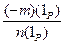Î Р₀ , 6. при m = 1, n = 1 получаем, что 1_PÎ Р₀ , 7. при m ¹ 0 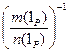= 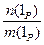Î Р₀ - при m < 0 здесь используется правило знаков из 6.2. Выполнение остальных свойств из определения поля в Р₀ следует из выполнения их в поле Р.

Подполе Р₀ - наименьшее, так как любое другое подполе Р₁ содержит Р₀. Отсюда следует, что Р₀ - простое подполе, так как оно не содержит собственных (меньших) подполей.

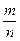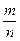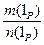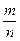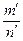Докажем, что поле Р₀ изоморфно полю Q. Определим отображение j: Q ® Р₀ так: пусть " Î Q по определению j()= Î Р₀. Тогда j - инъекция. В самом деле, если j()=j(), то 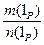= Þ m(1_Р)×n¢(1_Р) =

= m¢(1_Р)×n (1_Р) Þ (mn¢)(1_Р) =(m¢n)(1_Р)Þ (mn¢ - m¢n)(1_Р))=0_Р Þ

mn¢ - m¢n = 0 (так как char P = 0) Þ 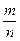= 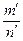. Сюръективность j очевидна. Таким образом, j - биекция. Сохранение операций при j следует из (*) и (**). Следовательно, j - изоморфизм.

ÿ

Теорема. Пусть Р – поле, и char P = р. Тогда

1) P содержит наименьшее (по включению) подполе Р₀,

2) подполе Р₀ – простое,

3) Р₀» Z_p.

Доказательство аналогично доказательству предыдущей теоремы 3.

Упражнение. Доказать эту теорему.

Лекция 13.

Date: 2015-09-25; view: 388; Нарушение авторских прав