Собственные колебания механической системы

С помощью уравнений Лагранжа можно исследовать колебания механической системы. Для систем с одной степенью свободы уравнение Лагранжа имеет вид:

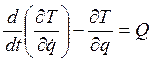, (20.1) где Q—обобщенная сила, равная . (20.2) Кинетическую и потенциальную энергию системы необходимо выразить обобщенные координаты и скорости

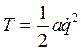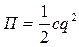; , (20.3) где 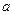-- приведенный коэффициент инерции;

с—приведенный коэффициент жесткости.

Для линейной обобщенной координаты коэффициент инерции 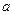имеет размерность массы. С учетом (20.2) и (20.3) получим дифференциальное уравнение малых собственных колебаний системы с одной степенью свободы

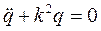, (20.4) где 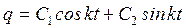. (20.5) Постоянные интегрирования С₁и С₂ определим из начальных условий (см. п. 5). Амплитуда колебаний зависит от начальных условий

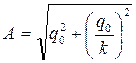, (20.6) где k—циклическая частота.

. (20.7) Период колебаний 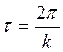. (20.8)

ПРИМЕР 30.

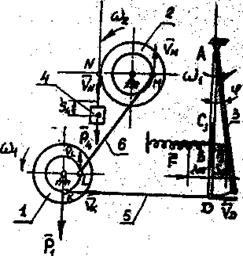
Механизм, расположенный в вертикальной плоскости (рис. 67) состоит из ступенчатых колес 1 и 2 с радиусами R₁=0,4м, r₁=0,2м, R₂=0,5м, r₂=0,3м, имеющими неподвижные оси вращения, однородного стержня 3 длиной 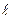=1,2м, закрепленного шарниром на одном из концов, груза 4, подвешенного к нити, намотанной на внешний обод колеса 2. На стержне расстояние АВ= 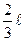(рис. 67). Стержень 3 соединен с колесом 1 невесомым стержнем 5. Колеса 1 и 2 соединены между собой невесомым стержнем 6. К стержню 3 в точке В прикреплена пружина жесткостью с=1000Н/см. Определить частоту и период малых колебаний системы около положения равновесия и статическую деформацию пружины 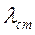, если известны массы тел m₁=16кг, m₃=8кг, m4=3кг.

РЕШЕНИЕ.

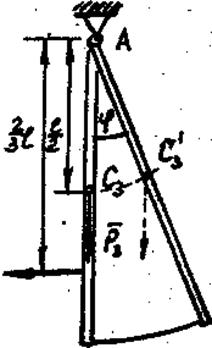
1. Рассмотрим произвольное положение системы, когда она выведена из состояния равновесия и совершает малые колебания. Система имеет одну степень свободы. принимаем за обобщенную координату угол 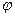отклонения стержня 3 от вертикали, считая угол 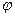малым. Составим уравнение Лагранжа в соответствии выбранной обобщенной координатой:

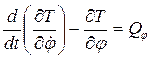. (1)

Рис. 67

2. Определим кинетическую энергию системы как сумму кинетических энергий тел, имеющих массу

Т=Т₁+Т₃+Т₄. (2)

Скорость вех тел, входящих в систему, выразим через обобщенную скорость . Стержень 3 вращается вокруг горизонтальной оси А с угловой скоростью . .

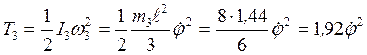Колесо 1 связано со стержнем 3 невесомым стержнем 5, тогда 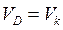или , откуда ;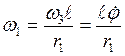

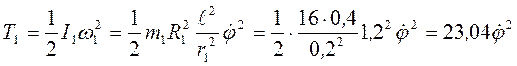. Груз 4 совершает поступательное движение, поэтому

;

;

;

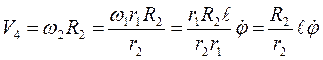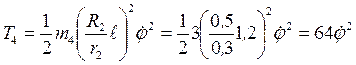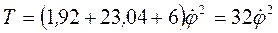. (3) Вычислим производные:

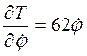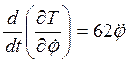; ; . (4)

3. Дадим системе возможное ускорение, при котором угол получит положительное приращение. Вычислим сумму элементарных работ всех действующих активных сил на соответствующих перемещениях.

Покажем активные силы, действующие на систему: 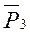, , 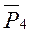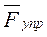. Работа сил 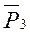и 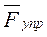равна моментам этих сил относительно точки О₁, работу силы 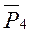вычисляем на перемещении :

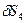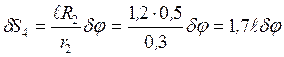
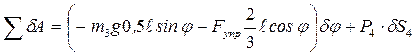. Сила упругости . Удлинение пружины равно 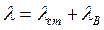, где -- удлинение пружины в начальном положении, соответствующем статическому равновесию; 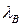- деформация пружины вследствие поворота стержня 3 на угол . .

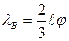Так как угол мал, можно принять , .

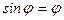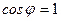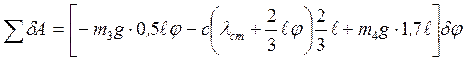. (6) Вычислим обобщенную силу

. (7) В положении равновесия =0, Q=0, тогда 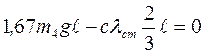, откуда

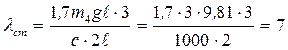см.

Подставляя значение 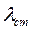в (7), находим обобщенную силу

.

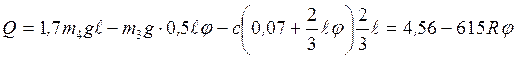После подстановки численных значений получим

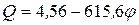. (8)

4. Составляем уравнение Лагранжа

или 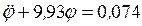(9) Уравнение (9) является дифференциальным уравнением собственных колебаний. Введем обозначение 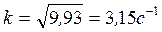, где k—циклическая частота.

Период колебаний .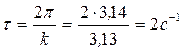

ЛИТЕРАТУРА

1.Законы, формулы, задачи физики. Справочник / Гофман Ю.В. - К.:
Внукова думка, 1977. - 576 с.

2.Яблонский А.А. Сборник заданий для курсовых работ во теоретической механике. - М.: Высшая школа, 1985. - 367 с,

3.Добронравов В.В., Никитин Н.Н. Курс теоретической механики.-
М.: Высшая школа, 1983. - 575 с.

4.Тарг СМ. Краткий курс теоретической механики. - М.: Высшая
школа, 1986. -416 с.

5. Никитин Н.Н. Курс теоретической механики. - М.: Высшая школа, 1990. - 607 с.

6. Файн Н.М. Сборник задач по теоретической механике. - М.:
Высшая школа, 1987. - 256 с.

7. Осадчий В.А., Файн А.Н. Руководство и решению задач по теоретической механике. -М.: Высшая школа, 1972. - 256 с.

8. Мовнин B.C., Израелит А.Б. Техническая механика. - Л.: Судостроение, 1971. - 344 с.

9. Бутенин Н.В., Лунц Я.Л., Меркин Д.Р. Курс теоретической меха­ники. Т.1,2. - М., 1985,

10. Мещерский И.В. Сборник задач по теоретической механике. - М.,
1986. - 480 с.

11.Сборник задач по теоретической механике /Под ред. К.С.Колесникова. -М.: Наука, 1989. - 448 с.

12.Бать М.И.,Джанелидзе Н.Ю., Кельзон А.С. Теоретическая механика в примерах в задачах. Ч .2. - М., 1984. - 624 с.

13.Теоретическая механика: Методические указания и контрольные
задания для студентов-заочников машиностроительных, строительных, транспортных, приборостроительных специальностей высших
учебных заведений /Л.И.Котова, Р.И.Надеева, С.М.Тарг и др. -
М.: Высшая школа, 1989, - 111 с.

14.Гернет М.М. Курс теоретической механики. - М.: Высшая школа,
1981. - 304 с.

15.Попов М.В. Теоретическая механика. - М.: Наука, I986. - 336с.

16.Зубов В.Г. Механика. - М.: Наука, 1976. - 352 с.

17.Стрелков С.П. Механика. - М.: Наука, 1975. - 560 с.

18.Старжинский В.М. Теоретическая механика. –М.: Наука, 1980. -464с.

19.Турбин Б.И., Рустамов С.И. Сборник задач по теоретической механике. -К.: Высшая школа, 1988. - 232с.

Date: 2015-09-24; view: 524; Нарушение авторских прав