
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Дифференциальные уравнения движения механической системы в обобщенных координатах (уравнение Лагранжа 2-го рода)
|
|
Обобщенными координатами qi называются независимые между собой параметры, с помощью которых можно определить положение всех точек механической системы. Число обобщенных координат равно числу степеней свободы S: q1, q2, …,qS. Положение всех точек кривошипно-ползунного механизма (рис. 63) зависит от одного параметра – угла поворота 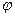 ведущего звена – кривошипа ОА.
ведущего звена – кривошипа ОА.
|
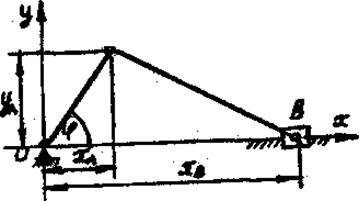 Рисунок 63
Рисунок 63
|
Следовательно, для этого механизма обобщенной координатой является угол 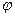 . Производная
. Производная 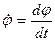 является обобщенной скоростью. Обобщенные координаты могут быть линейными (S,l,x,y) или угловыми (
является обобщенной скоростью. Обобщенные координаты могут быть линейными (S,l,x,y) или угловыми (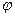 ,
, 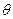 ), им будут соответствовать линейные или угловые обобщенные скорости.
), им будут соответствовать линейные или угловые обобщенные скорости.
|
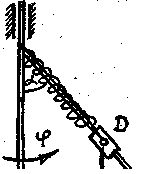 Рисунок 64
Рисунок 64
|
|
Число уравнений в системе (19.1) соответствует числу S степеней свободы. Величина Qi в правой части уравнения Лагранжа называется обобщенной силой. Для определения обобщенной силы системе необходимо дать возможное перемещение по соответствующей координате, вычислить сумму элементарных работ заданных сил на соответствующих перемещениях и разделить на приращение обобщенной координаты, т.е.  . (19.2)
. (19.2)
Если все силы, действующие на систему, являются потенциальными, то обобщенную силу можно вычислить по формуле 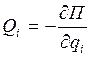 , (19.3) где П—потенциальная энергия системы.
, (19.3) где П—потенциальная энергия системы.
Если все обобщенные силы равны нулю, механическая система будет находиться в равновесии. Уравнения Лагранжа дают единый и достаточно простой метод решения задач динамики. Число уравнений не зависит от числа точек или тел, входящих в систему, и определяется числом степеней свободы. В уравнениях Лагранжа учитываются только активные силы, силы инерции и реакции связей в него не входят.
Решение задач с использованием уравнений Лагранжа нужно проводить в такой последовательности:
1. определить число степеней свободы механической системы;
2. выбрать систему координат и ввести независимые обобщенные координаты по числу степеней свободы системы; оси координат направить таким образом, чтобы при движении системы приращения обобщенных координат были положительными;
3. вычислить кинетическую энергию системы, выразив все переменные величины, входящие в формулу энергии, через обобщенные координаты и обобщенные скорости, т.е. 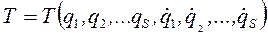 .
.
4. определить частные производные 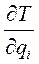 ,
,  ;
;
5. определить производные 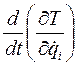 , считая, что все переменные, входящие в частную производную
, считая, что все переменные, входящие в частную производную 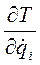 , являются функциями времени;
, являются функциями времени;
6. вычислить обобщенные силы, для чего
· изобразить все активные силы и реакции неидеальных связей, действующих на систему;
· дать независимые возможные перемещения по каждой обобщенной координате;
· вычислить сумму работ всех активных сил и реакций неидеальных связей на каждом возможном перемещении  , при этом все остальные возможные перемещения по остальным обобщенным координатам будут равны нулю;
, при этом все остальные возможные перемещения по остальным обобщенным координатам будут равны нулю;
· тогда обобщенная сила 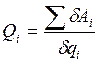 ;
;
7. подставить все найденные величины в уравнение Лагранжа;
8. решить уравнение Лагранжа в соответствии с условиями задачи.
ПРИМЕР 28.
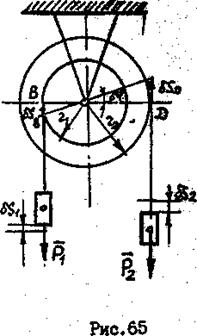
Барабаны радиусов r1 и r2, соединены между собой жестко, могут вращаться вокруг общей горизонтальной оси (рис. 65). На барабаны намотаны нерастяжимые нити, к концам которых подвешены груз А весом 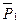 и груз В весом
и груз В весом 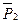 . Система движется под действием сил тяжести грузов. Определить угловое ускорение блока.
. Система движется под действием сил тяжести грузов. Определить угловое ускорение блока.
РЕШЕНИЕ.
1. Система имеет одну степень свободы: S=1. Принимаем за обобщенную координату угол поворота 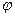 блоков вокруг горизонтальной оси, считая, что P1>P2.
блоков вокруг горизонтальной оси, считая, что P1>P2.
2. запишем уравнение Лагранжа 2-го рода с учетом выбранной обобщенной
|
|
Вычислим производные: 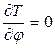 ;
; 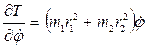 ;
;
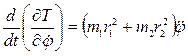 .
.
4. Дадим системе возможное перемещение по обобщенной координате 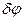 и вычислим сумму работ активных сил
и вычислим сумму работ активных сил 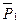 и
и 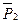 на соответствующих перемещениях
на соответствующих перемещениях 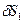 и
и 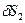 .
.
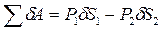 .
.
Перемещения 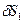 и
и 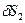 выразим через
выразим через 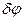 :
:
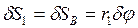 ;
;
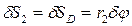 , тогда
, тогда 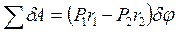 . Вычисляем обобщенную силу
. Вычисляем обобщенную силу 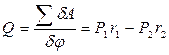 . (3) Подставим в уравнение (1) выражение (2) и (3):
. (3) Подставим в уравнение (1) выражение (2) и (3): 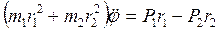 , откуда определим угловое ускорение блока
, откуда определим угловое ускорение блока 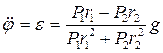 .
.
ПРИМЕР 29.
Механическая система состоит из тел 1, 2, 3 весом 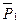 ,
, 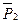 ,
, 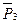 соответственно, связанных друг с другом нитями, намотанными на ступенчатые блоки 1 и 2 (рис.66). Радиусы ступенчатых блоков 1 и 2 равны соответственно R1=R, r1=0,4R1, R2=R, r2=0,8R. При вычислении моментов инерции блоки считать однородными сплошными цилиндрами радиуса R. На систему кроме сил тяжести действует пара сил с моментом М1=2РR, на участке АВ включена пружина с коэффициентом жесткости с, в начальный момент времени пружина не деформирована.
соответственно, связанных друг с другом нитями, намотанными на ступенчатые блоки 1 и 2 (рис.66). Радиусы ступенчатых блоков 1 и 2 равны соответственно R1=R, r1=0,4R1, R2=R, r2=0,8R. При вычислении моментов инерции блоки считать однородными сплошными цилиндрами радиуса R. На систему кроме сил тяжести действует пара сил с моментом М1=2РR, на участке АВ включена пружина с коэффициентом жесткости с, в начальный момент времени пружина не деформирована.
составить для системы уравнение Лагранжа и найти закон изменения обобщенной координаты х, т.е. х=f(t); считая, что движение начинается из состояния покоя, определить частоту и период колебаний, совершаемых телами системы при ее движении.
РЕШЕНИЕ.
 Рисунок 66
Рисунок 66
|
1. Рассматриваемая система имеет две степени свободы: S=2. Принимаем за обобщенные координаты угол поворота 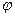 невесомого блока 1 и линейную координату х --удлинение пружины. Тогда уравнения Лагранжа для системы будут иметь вид:
невесомого блока 1 и линейную координату х --удлинение пружины. Тогда уравнения Лагранжа для системы будут иметь вид:
|
2. Определим кинетическую энергию системы как сумму кинетических энергий блока 2 и тележки 3: Т=Т1+Т3. (2) Блок 2 совершает вращательное движение вокруг неподвижной горизонтальной оси. Угловую скорость блок выразим через обобщенную координату 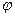 :
:
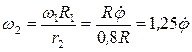 .
.
Момент инерции блок а2: 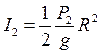 , тогда
, тогда
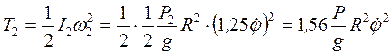 . (3) Движение тележки 4 зависит от изменения обобщенных координат
. (3) Движение тележки 4 зависит от изменения обобщенных координат 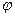 и х. Тележка совершает поступательное движение
и х. Тележка совершает поступательное движение
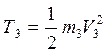 .
.
Для определения скорости V3 рассмотрим движение тележки как сложное, состоящее из относительного движения со скоростью 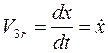 и переносного движения со скоростью
и переносного движения со скоростью 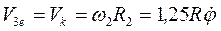 ;
;
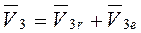 ;
;
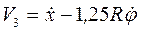 ;
;
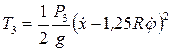 . (4) Подставим значения Т2 и Т3 из (3) и (4) в равенство (2):
. (4) Подставим значения Т2 и Т3 из (3) и (4) в равенство (2):
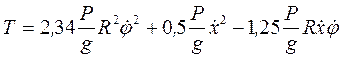 . (5)
. (5)
3. Дадим системе возможное перемещение по обобщенной координате 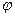 :
: 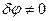 ,
, 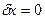 .
.
Вычислим производные: 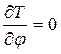 ;
;
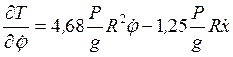 ;
;
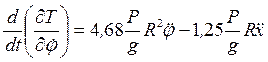 . (6) Вычислим сумму элементарных работ активных сил на возможном перемещении. На перемещении
. (6) Вычислим сумму элементарных работ активных сил на возможном перемещении. На перемещении 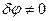 элементарную работу совершит момент М.
элементарную работу совершит момент М. 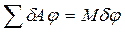 , тогда обобщенную силу можно определить по формуле:
, тогда обобщенную силу можно определить по формуле:
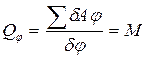 . (7) Так как обобщенная координата угловая, обобщенная сила является моментом. Составим первое уравнение Лагранжа:
. (7) Так как обобщенная координата угловая, обобщенная сила является моментом. Составим первое уравнение Лагранжа: 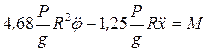 . (8) Учитывая, что по условию задачи М=2РR, получаем
. (8) Учитывая, что по условию задачи М=2РR, получаем 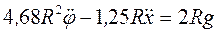 . (9)
. (9)
4. Дадим системе возможное перемещение по обобщенной координате х: 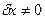 ,
, 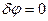 . Вычисли производные:
. Вычисли производные: 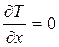 ;
;
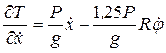 ;
;
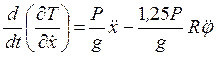 . (10) На возможном перемещении
. (10) На возможном перемещении 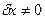 элементарную работу совершит сила упругости F=cx.
элементарную работу совершит сила упругости F=cx. 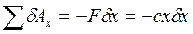 .
.
Вычислим обобщенную силу:  . (11) Составим второе уравнение Лагранжа
. (11) Составим второе уравнение Лагранжа 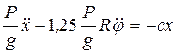 . (12) Таким образом, движение механической системы можно описать двумя дифференциальными уравнениями:
. (12) Таким образом, движение механической системы можно описать двумя дифференциальными уравнениями:
|
Из уравнения (13) выразим 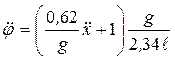 и, подставив в (14), получим
и, подставив в (14), получим
 или
или
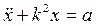 , (15) где
, (15) где 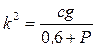 ;
; 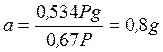 . Общее решение неоднородного дифференциального уравнения (15) имеет вид: х=х1+х2, где х1—общее решение однородного уравнения
. Общее решение неоднородного дифференциального уравнения (15) имеет вид: х=х1+х2, где х1—общее решение однородного уравнения 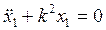 , т.е.
, т.е. 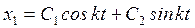 ; х2—частное решение уравнения (15) будем иметь в виде х2=В=const. Подставляя решение х2 в уравнение (15), получаем
; х2—частное решение уравнения (15) будем иметь в виде х2=В=const. Подставляя решение х2 в уравнение (15), получаем 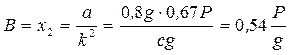 , тогда
, тогда
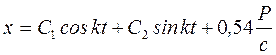 . (16) Постоянные интегрирования С1 и С2 определим из начальных условий,
. (16) Постоянные интегрирования С1 и С2 определим из начальных условий, 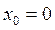 ,
, 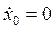 , продифференцировав равенство (16) по времени:
, продифференцировав равенство (16) по времени:
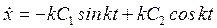 . (17) При t=0
. (17) При t=0 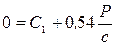 ; 0=kC2. Следовательно
; 0=kC2. Следовательно 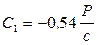 , С2=0. Окончательно получим искомую зависимость x=f(t) в виде:
, С2=0. Окончательно получим искомую зависимость x=f(t) в виде:
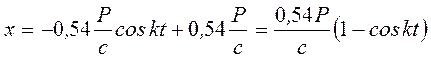 . (18) Таким образом, тележка совершает колебания согласно уравнению (18). Круговая частота этих колебаний
. (18) Таким образом, тележка совершает колебания согласно уравнению (18). Круговая частота этих колебаний 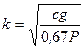 . Период колебаний
. Период колебаний 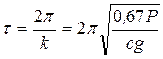 .
.
Date: 2015-09-24; view: 2095; Нарушение авторских прав
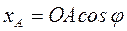 ;
;
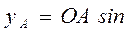 ;
;
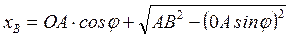
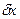 будут также независимы друг от друга.
будут также независимы друг от друга.
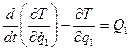 ,
,
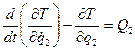 , (19.1)
………………….
, (19.1)
………………….
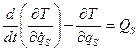
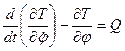 . (1)
3. Определим кинетическую энергию системы как сумму кинетических энергий грузов 1и 2:
Т=Т1+Т2. (2) Кинетическую энергию каждого груза выразим через обобщенную скорость
. (1)
3. Определим кинетическую энергию системы как сумму кинетических энергий грузов 1и 2:
Т=Т1+Т2. (2) Кинетическую энергию каждого груза выразим через обобщенную скорость 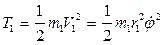 ;
;
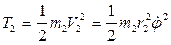 ;
;
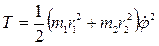 .
.
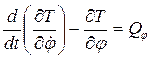 ; (1)
; (1)
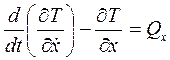 .
.
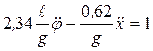 ; (13)
; (13)
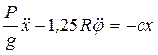 . (14)
. (14)