
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Принцип возможных перемещений
|
|
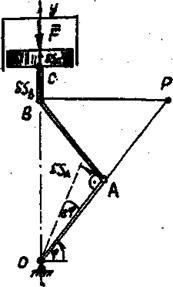 Рисунок 57
Рисунок 57
|
|
Так как возможные перемещения являются бесконечно малыми величинами, их можно считать линейными и направленными по скоростям соответствующих точек. Тогда для нахождения взаимосвязи между возможными перемещениями точек можно использовать метод мгновенного центра скоростей или теорему о проекциях скоростей двух точек на прямую, соединяющую эти точки, т.е. 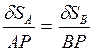 , (17.1) где
, (17.1) где 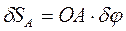 .
.
Идеальными называются наложенные на систему связи, работа реакций которых на возможном перемещении равна нулю. Такими связями являются неподвижная гладкая поверхность, цилиндрические и сферические шарниры, невесомые стержни.
Для того, чтобы механическая система с идеальными связями находилась в равновесии в данном положении, необходимо и достаточно, чтобы сумма элементарных работ всех активных сил, действующих на систему, на любом возможном перемещении точек системы равнялась нулю.
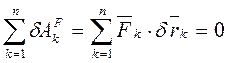 , (17.2) где
, (17.2) где 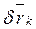 -- возможное перемещение произвольной точки Мк системы.
-- возможное перемещение произвольной точки Мк системы.
Используя принцип возможных перемещений, можно решать следующие задачи:
1. при заданном положении равновесия системы определить силы, действующие на систему, или найти зависимость между этими силами;
2. при заданных силах, действующих на систему, определить положение равновесия этой системы;
3. отбросить связи и, заменив их соответствующими реакциями орпеделить реакции связей.
При решении задач необходимо:
1. выделить систему, равновесия которой следует рассмотреть;
2. показать активные силы, действующие на систему;
3. составить уравнение принципа возможных перемещений (17.2);
4. решить полученное уравнение относительно искомой величины.
ПРИМЕР 24.
Определить величину усилия 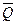 , способного удержать механизм (рис. 58) в положении равновесия, если на механизм действует окружное усилие
, способного удержать механизм (рис. 58) в положении равновесия, если на механизм действует окружное усилие 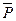 , момент трения
, момент трения 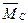 в опоре О2. Масса звеньев механизма равна m1, m2, m3, радиусы колес R1, r2, R2.
в опоре О2. Масса звеньев механизма равна m1, m2, m3, радиусы колес R1, r2, R2.
РЕШЕНИЕ.
1. Механизм, состоящий из колес 1 и 2 и груза 3, имеет одну степень свободы. Положение всех точек механизма зависит от угла поворота ведущего звена 1 под действием окружного усилия 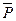 . На механизм действуют заданные силы
. На механизм действуют заданные силы 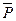 ,
, 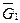 ,
,  ,
, 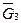 ,
, 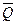 и момент сопротивления МС.
и момент сопротивления МС.
2. Дадим системе возможное перемещение: колеса 1 и 2 повернутся соответственно на углы 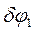 ,
,  , груз 3 опустится на
, груз 3 опустится на 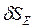 .
.
Выразим сумму работ всех активных сил на соответствующих возможных перемещениях:  . (1)
. (1)
|
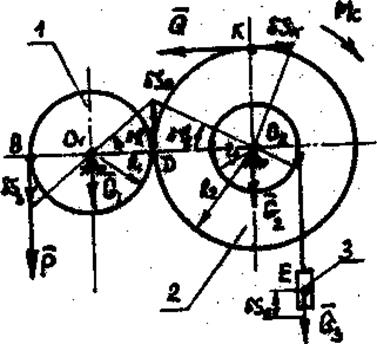 Рисунок 58
Рисунок 58
|
 . (2) Так как
. (2) Так как  , приравниваем нулю выражение
, приравниваем нулю выражение 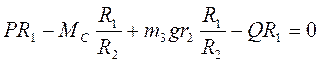 , (3) откуда выражаем силу Q:
, (3) откуда выражаем силу Q: 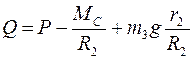 .
.
ПРИМЕР 25.
Механизм, расположенный в горизонтальной плоскости (рис. 59), находится под действием приложенных сил в равновесии, определяемым углами 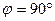 ,
, 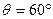 ,
, 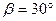 . Длины стержней механизма равны:
. Длины стержней механизма равны:  =0,4м,
=0,4м, 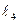 =0,6м, AE=ED. На ползун В механизма действует сила упругости пружины
=0,6м, AE=ED. На ползун В механизма действует сила упругости пружины  , где с=180н/см—коэффициент жесткости пружины,
, где с=180н/см—коэффициент жесткости пружины, 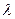 -- ее деформация. Кроме того, на ползун D действует сила Q=400Н, а на кривошип О1А – пара сил с моментом М=100Нм. Определить, чему равна при равновесии деформация
-- ее деформация. Кроме того, на ползун D действует сила Q=400Н, а на кривошип О1А – пара сил с моментом М=100Нм. Определить, чему равна при равновесии деформация 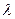 пружины.
пружины.
РЕШЕНИЕ.
1. Для нахождения деформации пружины используем принцип возможных перемещений, согласно которому 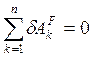 , (1) где
, (1) где 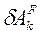 -- элементарная работа активных сил на соответствующих возможных перемещениях. Изображаем действующие на механизм активные силы:
-- элементарная работа активных сил на соответствующих возможных перемещениях. Изображаем действующие на механизм активные силы: 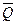 ,
, 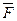 и пару сил с моментом М.
и пару сил с моментом М.
|
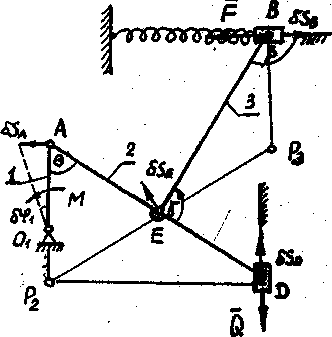 Рисунок 59
Рисунок 59
|
Взаимосвязь между перемещениями  и
и  найдем с помощью мгновенного центра скоростей звена 3. Так как
найдем с помощью мгновенного центра скоростей звена 3. Так как 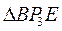 -- равнобедренный: ВР3=ЕР3;
-- равнобедренный: ВР3=ЕР3;  ;
; 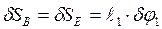 . (3) Составляем уравнение (1):
. (3) Составляем уравнение (1): 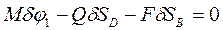 (4) или с учетом (2) и (3) получим
(4) или с учетом (2) и (3) получим  (5) или
(5) или 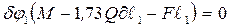 . Так как
. Так как 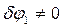 , то приравниваем нулю выражение
, то приравниваем нулю выражение  , откуда находим силу F:
, откуда находим силу F:  Н. Зная, что
Н. Зная, что 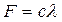 , находим деформацию пружины
, находим деформацию пружины 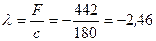 см.
см.
Знак минус указывает, что пружина сжата, а предварительно в расчете была принята растянутой.
Date: 2015-09-24; view: 1421; Нарушение авторских прав
 ведущего звена ОА. Кривошип ОА закреплен в точке О шарнирно. Возможным перемещением кривошипа ОА будет поворот на бесконечно малый угол
ведущего звена ОА. Кривошип ОА закреплен в точке О шарнирно. Возможным перемещением кривошипа ОА будет поворот на бесконечно малый угол  . Поршень движется в вертикальных направляющих, следовательно, возможные перемещения
. Поршень движется в вертикальных направляющих, следовательно, возможные перемещения 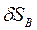 ,
, 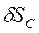 точек В и С штока, совершающее поступательное движение, направлены вдоль оси у.
точек В и С штока, совершающее поступательное движение, направлены вдоль оси у.
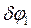 :
:  . Определим взаимосвязь между
. Определим взаимосвязь между  и
и 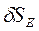 . Выразим возможное перемещение точки D:
. Выразим возможное перемещение точки D: 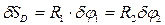 ; откуда
; откуда  ;
;  .
С учетом полученных соотношений уравнение (1) примет вид:
.
С учетом полученных соотношений уравнение (1) примет вид:
 -- поворот стержня 1 вокруг оси О1;
-- поворот стержня 1 вокруг оси О1;  . Взаимосвязь между перемещениями
. Взаимосвязь между перемещениями 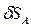 ,
, 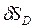 ,
, 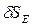 найдем с помощью мгновенного центра скоростей звена 2:
найдем с помощью мгновенного центра скоростей звена 2: 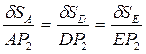 . Так как
. Так как 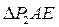 -- равносторонний:
-- равносторонний: 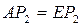 , следовательно,
, следовательно, 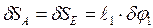 ;
;  . (2)
. (2)