
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Дифференциальные уравнения движения твердого тела
|
|
Из общих теорем динамики можно получить дифференциальные уравнения движения твердого тела. При поступательном движении твердого тела все его точки движутся так же, как и центр масс. Поэтому дифференциальные уравнения поступательного движения получим из теоремы о движении центра масс: 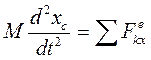 ;
; 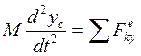 ;
;  , (14.1) где М—масса тела;
, (14.1) где М—масса тела;
xc, yc, zc, -- координаты центра масс тела;
 ,
, 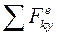 ,
,  -- проекция главного вектора внешних сил на оси координат. Используя дифференциальные уравнения (14.1), можно решать две задачи динамики поступательного движения твердого тела:
-- проекция главного вектора внешних сил на оси координат. Используя дифференциальные уравнения (14.1), можно решать две задачи динамики поступательного движения твердого тела:
1. по заданным уравнениям движения тела определять главный вектор внешних сил, приложенных к твердому телу;
2. по заданным внешним силам, действующим на тело, и известным начальным условиям определять закон движения тела, если оно движется поступательно;
Таким образом, изучение поступательного движения твердого тела сводится к изучению движения одной его точки – центра масс тела.
Из теоремы об изменении кинетического момента системы относительно оси (10.15) с учетом (10.6) можно получить дифференциальное уравнение вращательного движения твердого тела  или
или 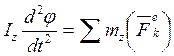 . (14.2) Уравнение (14.2) представляет собой дифференциальное уравнение вращательного движения твердого тела, с помощью которого можно решать следующие задачи:
. (14.2) Уравнение (14.2) представляет собой дифференциальное уравнение вращательного движения твердого тела, с помощью которого можно решать следующие задачи:
1. по заданному уравнению вращения тела 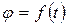 и известному моменту инерции
и известному моменту инерции  определять главный момент внешних сил, действующих на тело:
определять главный момент внешних сил, действующих на тело:  ;
;
2. по заданным внешним силам, приложенным к телу, и известным начальным условиям вращения  и
и 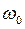 и моменту инерции
и моменту инерции  находить уравнение вращения тела
находить уравнение вращения тела 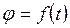 ;
;
3. по заданному закону вращательного движения тела 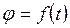 и известному моменту внешних сил
и известному моменту внешних сил 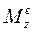 определять момент инерции тела
определять момент инерции тела  относительно оси вращения.
относительно оси вращения.
Если к твердому телу приложен постоянно действующий момент внешних сил, то угловое ускорение тела также будет постоянным, т.е. может вращаться равноускоренно или равнозамедленно. Решение задачи целесообразно проводить в следующем порядке:
1. изобразить тело, вращение которого рассматривается;
2. приложить все активные силы и моменты, действующие на тело;
3. освободить тело от связей, заменив их реакциями;
4. составить уравнение вращательного движения;
5. решить полученное уравнение в соответствии с условием задачи.
ПРИМЕР 19.
 Рисунок 46
Рисунок 46
|
|
РЕШЕНИЕ.
1. На вал действует сила тяжести  , вращающий момент Мвр, момент трения в опорах Мтр, реакции опор
, вращающий момент Мвр, момент трения в опорах Мтр, реакции опор  ,
, 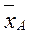 ,
,  ,
,  , натяжение ведущей
, натяжение ведущей 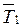 и ведомой
и ведомой 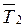 ветвей ремня.
ветвей ремня.
2. Составим дифференциальное уравнение вращательного движения вала 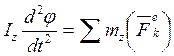 . (1) Момент инерции
. (1) Момент инерции  кгм2. Момент внешних сил относительно оси вращения
кгм2. Момент внешних сил относительно оси вращения 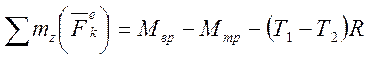 . (2) Зная закон вращательного движения, определим угловое ускорение вала
. (2) Зная закон вращательного движения, определим угловое ускорение вала 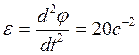 . (3) Выразим момент трения в опорах из уравнения (2) с учетом (1) и (3):
. (3) Выразим момент трения в опорах из уравнения (2) с учетом (1) и (3):
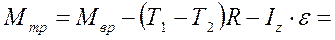
 Нм.
Нм.
Так как плоское движение твердого тела состоит из поступательного движения с центром масс и вращения вокруг оси, проходящей через центр масс, то дифференциальные уравнения плоского движения твердого тела имеют вид: 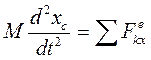 ;
; 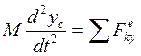 ;
; 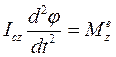 . (14.3) Первые два уравнения описывают поступательную часть движения тела вместе с центром масс. Третье уравнение выражает закон вращения тела вокруг оси, проходящей через центр масс. При решении задач динамики плоского движения твердого тела необходимо:
. (14.3) Первые два уравнения описывают поступательную часть движения тела вместе с центром масс. Третье уравнение выражает закон вращения тела вокруг оси, проходящей через центр масс. При решении задач динамики плоского движения твердого тела необходимо:
1. изобразить все внешние силы, приложенные к телу;
2. выбрать систему координат и определить положительное направление отсчета угла поворота  ;
;
3. составить дифференциальные уравнения плоского движения твердого тела;
4. решить систему уравнений в соответствии с условием задачи.
ПРИМЕР 20.

|
|
трения f о плоскость, при котором возможно качение без скольжения. Барабан рассматривать как сплошной однородный цилиндр радиуса R.
РЕШЕНИЕ.
1. Барабан совершает плоскопараллельное движение под действием заданных сил: 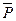 ,
,  и момента М. Полная реакция шероховатой поверхности состоит из нормального давления
и момента М. Полная реакция шероховатой поверхности состоит из нормального давления 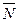 и силы трения
и силы трения  , направленной вдоль горизонтальной шероховатой поверхности. Так как направление движения барабана под действием приложенных сил заранее не известно, направление силы трения показываем произвольно.
, направленной вдоль горизонтальной шероховатой поверхности. Так как направление движения барабана под действием приложенных сил заранее не известно, направление силы трения показываем произвольно.

|
или  ; (2)
; (2)
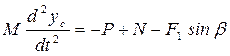 ; (3)
; (3)
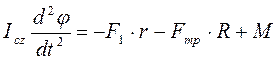 . (4)
. (4)
3. Определение уравнение движения центра масс барабана. Так как 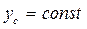 ,
,  , то уравнение (2), (3) и (4) содержат 4 неизвестных величины: N, Fтр,
, то уравнение (2), (3) и (4) содержат 4 неизвестных величины: N, Fтр, 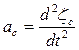 ,
, 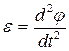 . Так как центр масс барабана движется по прямолинейной траектории,
. Так как центр масс барабана движется по прямолинейной траектории,  . Мгновенный центр скоростей барабана находится в точке В:
. Мгновенный центр скоростей барабана находится в точке В: 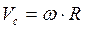 ;
; 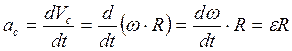 ; следовательно,
; следовательно,  . (5) Момент инерции однородного цилиндра
. (5) Момент инерции однородного цилиндра 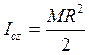 . Подставив (5) в (4), и разделив на R, получим
. Подставив (5) в (4), и разделив на R, получим 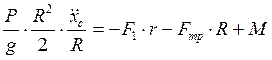 ;
;
 . (6) Сложив равенства (2) и (6), получим
. (6) Сложив равенства (2) и (6), получим  (7) или
(7) или 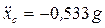 . (8) Дважды проинтегрируем уравнение (8):
. (8) Дважды проинтегрируем уравнение (8): 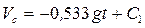 ; (9)
; (9)
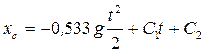 . (10) Постоянные интегрирования С1 и С2 определим из начальных условий:
. (10) Постоянные интегрирования С1 и С2 определим из начальных условий:
при t=0; VC0=0; C1=0;
xC0=0; C2=0. Окончательное уравнение движения центра масс барабана имеет вид: хс=-0,266gt2. (11) Знак «-» показывает, что движение барабана происходит в направлении противоположном положительному направлению оси х.
4. Определение fmin.
При качении без скольжения сила трения удовлетворяет неравенству:  . (12) Величину нормального давления N определим из уравнения (3):
. (12) Величину нормального давления N определим из уравнения (3):  ;
; 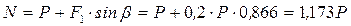 . Значение силы трения Fтр определим из уравнения (6), подставив в него значение
. Значение силы трения Fтр определим из уравнения (6), подставив в него значение  :
: 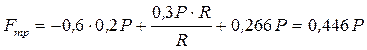 . Подставляя полученное значение силы трения в неравенство (12), получим
. Подставляя полученное значение силы трения в неравенство (12), получим 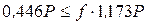 , откуда
, откуда 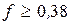 . Следовательно, наименьшее значение коэффициента трения, при котором возможно качение барабана без скольжения fmin=0,38.
. Следовательно, наименьшее значение коэффициента трения, при котором возможно качение барабана без скольжения fmin=0,38.
Date: 2015-09-24; view: 1165; Нарушение авторских прав
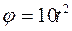 , радиус шкива R=0,25м, масса вала со шкивом m=5кг и радиус инерции
, радиус шкива R=0,25м, масса вала со шкивом m=5кг и радиус инерции  =0,15м.
=0,15м.
 . Кроме силы
. Кроме силы  и наименьшее значение коэффициента
и наименьшее значение коэффициента
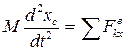 ;
;
 ; (1)
; (1)
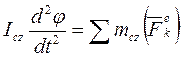 .
.