
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Теорема об изменении киннетической энергии системы
|
|
Кинетическая энергия механической системы равна сумме кинетических энергий всех материальных точек, входящих в систему 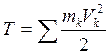 , (13.1) где mk,Vk—соответственно масса и скорость произвольной точки Мk системы.
, (13.1) где mk,Vk—соответственно масса и скорость произвольной точки Мk системы.
Теорему об изменении кинетической энергии механической системы можно использовать в дифференциальной (13.2) или конечной (интегральной) (13.3) форме. Дифференциал кинетической энергии системы равен сумме элементарных работ всех внешних и внутренних сил, действующих на систему
 . (13.2) Изменение кинетической энергии механической системы на каком-то перемещении равно сумме работ всех внешних и внутренних сил, действующих на систему, на том же перемещении
. (13.2) Изменение кинетической энергии механической системы на каком-то перемещении равно сумме работ всех внешних и внутренних сил, действующих на систему, на том же перемещении 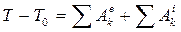 , (13.3) где Т0, Т – соответственно кинетическая энергия в начале и конце перемещения системы.
, (13.3) где Т0, Т – соответственно кинетическая энергия в начале и конце перемещения системы.
Кинетическая энергия твердого тела зависит от вида движения, совершаемого телом. При поступательном движении все точки твердого тела движутся со скоростью, равной скорости 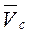 центра масс тела. Тогда
центра масс тела. Тогда 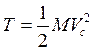 , (13.4) где М—масса тела.
, (13.4) где М—масса тела.
Для тела, вращающегося вокруг неподвижной оси с угловой скоростью 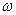 , мерой инертности является момент инерции
, мерой инертности является момент инерции  тела относительно оси вращения. Следовательно, кинетическая энергия вращающегося тела
тела относительно оси вращения. Следовательно, кинетическая энергия вращающегося тела 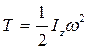 . (13.5)
. (13.5)
Плоское движение твердого тела можно рассматривать состоящим из поступательного движения с центром масс и вращением вокруг оси, проходящей через центр масс. Кинетическая энергия тела при плоском движении будет представлена двумя слагаемыми 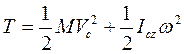 , (13.6) где
, (13.6) где 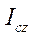 -- момент инерции тела относительно оси вращения, проходящей через центр масс тела.
-- момент инерции тела относительно оси вращения, проходящей через центр масс тела.
Сферическое движение твердого тела можно рассматривать как вращение вокруг мгновенной оси вращения. Тогда 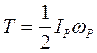 , (13.7) где
, (13.7) где 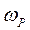 -- мгновенная угловая скорость тела;
-- мгновенная угловая скорость тела;
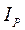 -- момент инерции тела относительно мгновенной оси вращения.
-- момент инерции тела относительно мгновенной оси вращения.
В общем случае движения свободное твердое тело движется поступательно вместе с центром масс и вращается вокруг мгновенной оси, проходящей через центр масс. Тогда 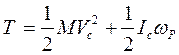 , (13.8) где
, (13.8) где 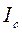 -- момент инерции тела относительно мгновенной оси, проходящей через центр масс тела.
-- момент инерции тела относительно мгновенной оси, проходящей через центр масс тела.
Если механическая система образована из нескольких твердых тел, кинетическая энергия системы равна сумме кинетических энергий всех тел системы, имеющих массу
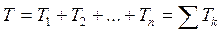 . (13.9) Если в начальный момент механическая система находясь в покое, то Т0=0. Для неизменяемой механической системы работа внутренних сил
. (13.9) Если в начальный момент механическая система находясь в покое, то Т0=0. Для неизменяемой механической системы работа внутренних сил 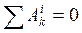 .
.
ПРИМЕР 18.
 Рисунок 45
Рисунок 45
|
|
Определить угловую скорость 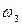 блока 3 в тот момент времени, когда перемещение S1=0,2м, при следующих исходных данных: m1=4кг, m3=2,5кг, m4=6кг, с=320Н/м,
блока 3 в тот момент времени, когда перемещение S1=0,2м, при следующих исходных данных: m1=4кг, m3=2,5кг, m4=6кг, с=320Н/м, 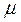 =1,4Н/м, F=50(9+2S).
=1,4Н/м, F=50(9+2S).
РЕШЕИЕ.
1. Неизменяемая механическая система состоит из тел 1, 3, 4 с известными массами и невесомого блока 2. На систему действуют внешние силы: активные 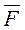 ,
, 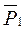 ,
, 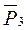 ,
, 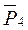 ,
, 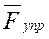 , реакции
, реакции 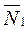 ,
,  , сила трения
, сила трения 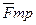 и момент М. Для определения угловой скорости
и момент М. Для определения угловой скорости 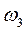 блок а3 применим теорему об изменении кинетической энергии неизменяемой механической системы
блок а3 применим теорему об изменении кинетической энергии неизменяемой механической системы 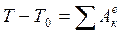 . (1) Так как система начала движения из состояния покоя, то Т0=0.
. (1) Так как система начала движения из состояния покоя, то Т0=0.
2. Кинетическая энергия системы равна сумме кинетических энергий всех тел системы, имеющих массу: Т=Т1+Т3+Т4. (2) Кинетическую энергию всех тел системы выражаем с учетом вида движения каждого тела. Груз 1 движется поступательно, блок 3 вращается вокруг неподвижной оси. Подвижный блок 4 совершает плоское движение
|

I3, I4 – момент инерции относительно осей вращения блоков 3 и 4.
Все скорости выразим через искомую угловую скорость 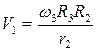 ;
; 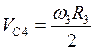 ;
; 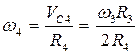 . (3) Моменты инерции блоков (3) и (4) определяем с учетом распределения масс
. (3) Моменты инерции блоков (3) и (4) определяем с учетом распределения масс  ;
; 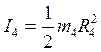 . (4) Подставим (3) и (4) в равенства (2)
. (4) Подставим (3) и (4) в равенства (2)
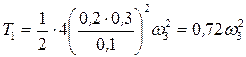 ;
;
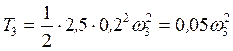 ; (5)
; (5)
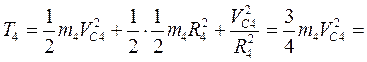
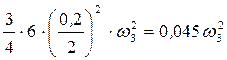 .
.
С учетом равенства (2) получим 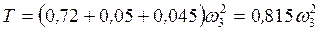 . (6)
. (6)
3. Определим сумму работ всех действующих внешних сил на том перемещении, которое будет иметь система, когда груз 1 пройдет путь S1.  . (7) Работа сил
. (7) Работа сил 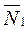 ,
, 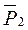 ,
,  ,
, 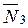 ,
, 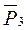 равна нулю, так как реакция
равна нулю, так как реакция 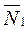 перпендикулярна перемещению груза, а остальные силы приложены к неподвижным точкам. Вычисляем работу заданных сил на перемещениях точек их приложения, которые выразим через перемещение груза S1:
перпендикулярна перемещению груза, а остальные силы приложены к неподвижным точкам. Вычисляем работу заданных сил на перемещениях точек их приложения, которые выразим через перемещение груза S1:  дж;
дж; 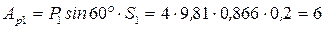 дж;
дж;  дж;
дж;  дж;
дж;
где 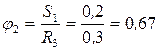 ;
; 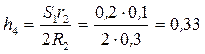 м;
м; 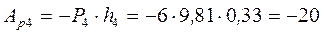 дж;
дж;  дж, где
дж, где 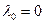 ;
; 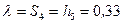 . С учетом равенства (7) получим:
. С учетом равенства (7) получим:
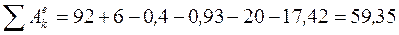 дж. (8) Подставим (6) и (8) в (1):
дж. (8) Подставим (6) и (8) в (1): 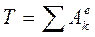 ;
;
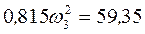 , откуда
, откуда 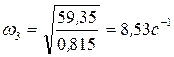 .
.
Date: 2015-09-24; view: 461; Нарушение авторских прав
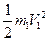 ;
Т3=
;
Т3= 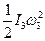 ; (3)
Т4=
; (3)
Т4=  .
.