
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Общее уравнение динамаики
|
|
Принцип возможных перемещений дает общий метод решения задач статики. Принцип Даламбера использует методы статики для решения задач динамики. Применяя два эти принципа одновременно, можно получить общий метод решения задач динамики.
|
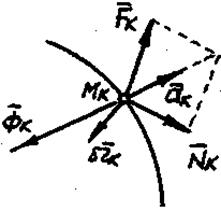 Рисунок 60
Рисунок 60
|
При наличии сил трения их нужно причислить к задаваемым силам. С помощью общего уравнения динамики можно определять силы по заданному движению (прямая задача динамики) или определять движение по заданным силам (обратная задача динамики). Для решения задач с помощью общего уравнения динамики необходимо:
1. показать на схеме активные силы и реакции неидеальных связей (например, силы трения);
2. добавить к активным силам силы инерции;
3. дать возможное перемещение точкам системы, выражая перемещение всех точек через возможное перемещение одной из точек системы;
4. составить общее уравнение динамики, вычисляя сумму элементарных работ всех активных сил и сил инерции на возможном перемещении точки их приложения;
5. решить полученное уравнение в соответствии с условием задачи
ПРИМЕР 26.
|
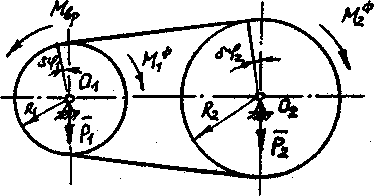 Рисунок 61
Рисунок 61
|
РЕШЕНИЕ.
1. Массы шкивов равномерно распределены по их ободам и пропорциональны размерам:

|

где  -- плотность материала шкивов. Используя выражение (1), можно определить размер второго шкива
-- плотность материала шкивов. Используя выражение (1), можно определить размер второго шкива
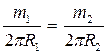 ;
;  м.
м.
2. Силы инерции точек шкивов приводятся к моментам сил инерции, которые соответственно равны  ; (2)
; (2)
 . (3)
. (3)
Угловые ускорения колес обратно пропорциональны их радиусам, т.е.
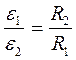 или
или 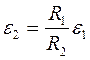 . Тогда
. Тогда 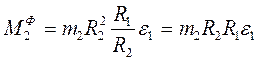 . (4)
. (4)
3. Запишем общее уравнение динамики  . (5) Дадим системе возможное перемещение: шкив 1 повернется на угол
. (5) Дадим системе возможное перемещение: шкив 1 повернется на угол 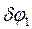 , шкив 2—на угол
, шкив 2—на угол  . Вычислим работу активных сил и сил инерции на возможном перемещении системы
. Вычислим работу активных сил и сил инерции на возможном перемещении системы 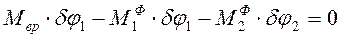 . (6) Выразим возможное перемещение
. (6) Выразим возможное перемещение  шкива 2 через
шкива 2 через 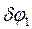 :
: 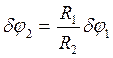 . Тогда, с учетом (2) и (4), получим:
. Тогда, с учетом (2) и (4), получим:  . (7) Так как
. (7) Так как  , приравниваем нулю выражение
, приравниваем нулю выражение 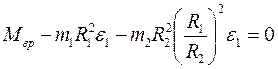 , из которого находим угловое ускорение шкива 1:
, из которого находим угловое ускорение шкива 1:  с-2.
с-2.
ПРИМЕР 27.
Механическая система состоит из однородных ступенчатых шкивов 1 и 2, обмотанных нитями, грузов 3, 4 и 5, прикрепленных к этим нитям, и невесомого блока 2. Система движется в вертикальной плоскости под действием сил тяжести и пары сил с моментом М=12Нм., приложенных к шкиву 1. Радиусы ступеней шкива равны: R1=0,2м, r1=0,1м, а шкива 2—R2=0,3м и r2=0,15м;радиус инерции шкива 1 относительно оси вращения 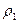 =0,1м (рис. 62). Пренебрегая трением, определить ускорение груза 3, если Р1=30Н, Р3=40Н, Р4=20Н, Р5=10Н.
=0,1м (рис. 62). Пренебрегая трением, определить ускорение груза 3, если Р1=30Н, Р3=40Н, Р4=20Н, Р5=10Н.
РЕШЕНИЕ.
1. Рассмотрим движение механической системы, состоящей из тел 1, 2, 3, 4, 5, соединенных нитями. Система имеет одну степень свободы. Связи, наложенные на тела системы, относятся к идеальным. Для определения ускорения груза 3 применим общее уравнение динамики:
 Рисунок 62
Рисунок 62
|
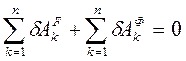 , (1) где
, (1) где  -- сумма элементарных работ активных сил;
-- сумма элементарных работ активных сил;
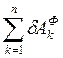 -- сумма элементарных работ сил инерции.
-- сумма элементарных работ сил инерции.
2. Покажем активные силы:  ,
, 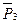 ,
,  ,
,  и пару сил с моментом М. Зададим направление ускорения груза 3 и покажем силы инерции
и пару сил с моментом М. Зададим направление ускорения груза 3 и покажем силы инерции 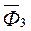 ,
, 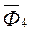 ,
, 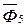 и момент сил инерции
и момент сил инерции  :
: 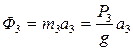 ;
;
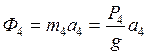 ;
;
 ; (2)
; (2)
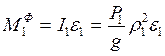 .
.
3. Дадим системе возможное перемещение и составим уравнение (1). 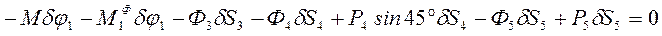 . Выразим все перемещения через
. Выразим все перемещения через  :
:  ;
;
 ;
;
 ; (3)
; (3)
 . С учетом выражений (2) и (3) уравнение (1) примет вид:
. С учетом выражений (2) и (3) уравнение (1) примет вид: 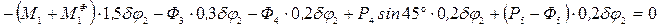 (4) или
(4) или 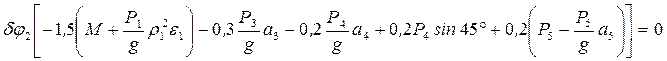 . (5)
. (5)
Выразим 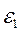 ,
, 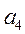 ,
, 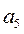 через искомое ускорение груза
через искомое ускорение груза  :
:
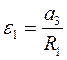 ;
;  ;
;  . (6) Так как
. (6) Так как 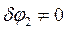 , с учетом (6) приравниваем нулю выражение (5):
, с учетом (6) приравниваем нулю выражение (5): 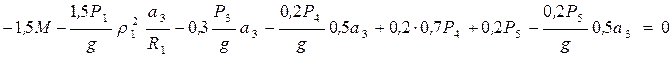 . Откуда определим ускорение
. Откуда определим ускорение  груза 3:
груза 3:  .
.
Date: 2015-09-24; view: 478; Нарушение авторских прав
 (18.1) или
(18.1) или 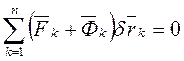 . (18.2)
. (18.2)
 ; (1)
; (1)
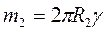 ,
,