Решение первой задачи динамики

При решении первой задачи динамики можно использовать дифференциальные уравнения движения точки в векторной, координатной и естественной форме. Решение задачи необходимо осуществлять в следующем порядке:

1. изобразить точку в текущий момент времени;

2. показать активные (заданные) силы, действующие на точку;

3. освободить точку от связей, заменяя действие связей реакциями;

4. выбрать систему координат, если она не указана в задаче;

5. составить дифференциальные уравнения движения точки в выбранной системе координат;

6. по заданным уравнениям движения определить проекции ускорения на оси координат;

7. из дифференциальных уравнений движения определить проекции силы, действующей на точку.

РЕШЕНИЕ ПЕРВОЙ ЗАДАЧИ ДИНАМИКИ ДЛЯ СВОБОДНОЙ МАТЕРИАЛЬНОЙ ТОЧКИ

ПРИМЕР 1.

Материальная точка массой m движется по окружности радиуса R согласно уравнению OM=S=Re^2t (рис. 2). Определить величину равнодействующей сил, приложенных к точке, как функцию времени.

РЕШЕНИЕ.

1. Так как точка движется по криволинейной траектории, используем дифференциальные уравнения движения точки в проекциях на естественные оси: касательную 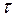и нормаль :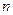

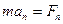, . (1)

2. Выразим из закона движения точки проекции ускорения на естественные оси

;

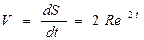
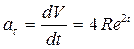; (2)

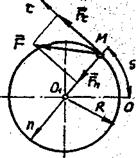Рисунок 2

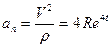. (3)

Подставим (2) и (3) в (1), выразим проекции силы

на естественные оси:

; .

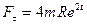Силу, действующую на точку, выразим через ее

проекции на естественные оси

.

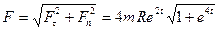РЕШЕНИЕ ПЕРВОЙ ЗАДАЧИ ДЛЯ НЕСВОБОДНОЙ МАТЕРИАЛЬНОЙ ТОЧКИ

ПРИМЕР 2.

Определить давление автомобиля весом Р=10000Н, движущегося с постоянной скоростью 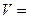36км/ч по мосту с радиусом кривизны 20м, если автомобиль находится в центре вогнутого (рис. 3,а) и выпуклого (рис. 3,б) моста.

Рисунок 3

РЕШЕНИЕ.

1. Применим дифференциальное уравнение движения точки в проекции на нормаль n:

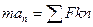
, (1)

где 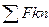-- сумма проекций на нормаль заданных сил и реакций связей;

для схемы а):

;

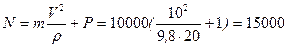Н;

для схемы б):

;

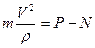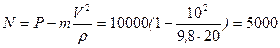Н.

Date: 2015-09-24; view: 692; Нарушение авторских прав