Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Однофакторный дисперсионный анализ
|
|
В рамках изучения связи признаков часто возникает вопрос о том, какой из признаков влияющий (причина), а какой — зависимый (следствие). В статистике выработан ряд методов, позволяющих выделить факторы (влияющие переменные) и отклики (переменные под влиянием).
Существенную роль играет анализ разброса значений признака — их отклонений от среднего. В основе этого подхода лежит соображение о том, что, если фактор действительно оказывает влияние на отклик, то на разных уровнях фактора (т.е. при разных значениях влияющей переменной) будут наблюдаться разные средние значения отклика. Ясно, что говорить о наличии влияния можно только в том случае, если разброс значений признака в группах меньше общего разброса значений.
Следовательно, степень влияния фактора на отклик может оцениваться как отношение разброса значений отклика между группами к разбросу значений во всех группах относительно генеральной средней (средней по всем группам).
Пусть исходная совокупность делится на J однородных групп по одному фактору (т.е. фактор с J уровнями), в каждой по 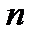 элементов:
элементов:
| Номер испытания, i | Уровни фактора, j | |||
| ... | J | |||


| 
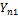
| 
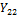
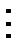

| …
…
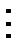 ...
...
| 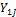


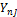
|
| Групповые средние | 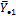
| 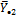
| … | 
|
Сначала находятся J частных средних в каждой группе:

Далее, определяется общая средняя как средняя арифметическая этих частных средних:

Затем, вводятся три величины:
внутригрупповая сумма квадратов (sum of squares within group):
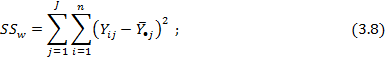
межгрупповая сумма квадратов (sum of squares between groups):
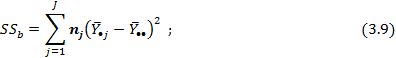
общая сумма квадратов (total sum of squares):
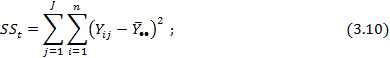
где J — число уровней фактора (групп);
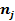 — объем j -ой группы;
— объем j -ой группы;
 — внутригрупповая средняя;
— внутригрупповая средняя;
 — общая средняя для всей совокупности.
— общая средняя для всей совокупности.
Несложно доказать, что
SSt= SSw + SSb.
Однофакторный дисперсионный анализ — метод, позволяющий на основании проверки гипотезы о равенстве средних делать выводы о направленном влиянии (одного) фактора на зависимый признак.
Модель однофакторного дисперсионного анализа выражает предположение о том, из чего значение зависимого признака (Y), и записывается следующим образом:
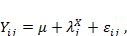
где μ — некий средний уровень по всей изучаемой совокупности, на фоне которого изучается действие фактора (X) на зависимый признак (Y);  — вклад в формирование значения зависимого признака j -го уровня фактора (X) (модель);
— вклад в формирование значения зависимого признака j -го уровня фактора (X) (модель);  — случайная добавка, (ошибка модели). Данная запись действительна для генеральной совокупности, на выборочной совокупности генеральные параметры заменяются выборочными оценками. Подставив выборочные оценки в уравнение, получим:
— случайная добавка, (ошибка модели). Данная запись действительна для генеральной совокупности, на выборочной совокупности генеральные параметры заменяются выборочными оценками. Подставив выборочные оценки в уравнение, получим:
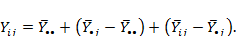
Все три элемента модели можно расценить как вклады в вариацию признака Y, как источники такой вариации.
Нулевой статистической гипотезой дисперсионного анализа является равенство средних значений зависимого признака при разных уровнях фактора:
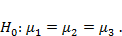
Заметим, что альтернативная гипотеза 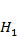 здесь формулируется достаточно неопределенно —
здесь формулируется достаточно неопределенно — 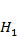 : не все средние равны.
: не все средние равны.
Каждой сумме квадратов отвечает свое число степеней свободы:
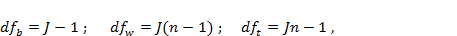
где J – количество уровней фактора; n – количество измеренийпри каждом уровне фактора.
Заметим, что
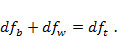
Введем обозначения
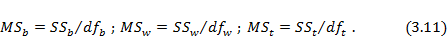
MSb, MSw, MSt — средние квадраты: межгрупповой, внутригрупповой и общий ( mean square between/within/total).
Искомая статистика (критерий Фишера) имеет вид

Чем больше влияние факторного (группировочного) признака на результативный, тем больше значение F.
Расчетное значение F сравнивается с критическим 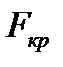 , определяемым по таблице в зависимости от числа степеней свободы и уровня значимости
, определяемым по таблице в зависимости от числа степеней свободы и уровня значимости 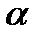 . Если
. Если 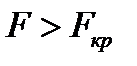 , то факторный признак оказывает влияние на исследуемый признак. Если
, то факторный признак оказывает влияние на исследуемый признак. Если 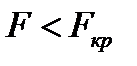 , то только с вероятностью не выше чем
, то только с вероятностью не выше чем 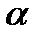 случайные значения величины
случайные значения величины  будут превышать расчетное значение. Следовательно, с малой вероятностью
будут превышать расчетное значение. Следовательно, с малой вероятностью 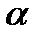 факторный признак будет оказывать влияние на результативный признак и это влияние можно не учитывать.
факторный признак будет оказывать влияние на результативный признак и это влияние можно не учитывать.
Соотношение межгруппового и общего средних квадратов называется коэффициентом детерминации 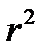 и показывает, какая доля в общей дисперсии приходится на дисперсию, обусловленную вариацией признака, положенного в основу группировки:
и показывает, какая доля в общей дисперсии приходится на дисперсию, обусловленную вариацией признака, положенного в основу группировки:

Пример 3.2. Банк имеет по четыре отделения в трех городах. Текущие объемы денежных вкладов (в условных единицах) представлены в таблице:
Можно ли утверждать на уровне значимости Вычисляем групповые средние Межгрупповая (факторная) сумма квадратов (3.9):
Внутригрупповая (остаточная) сумма квадратов (3.8):
Общая сумма квадратов: SSt= SSw + SSb =204+224=428. Степени свободы равны:
Статистика (критерий) Фишера:
Для Полученный коэффициент детерминации (3.22):
показывает, что дисперсия зависит от места расположения отделений на 52,3%; остальные же 47,7 % объясняются множеством других неучтенных факторов. |
Date: 2015-09-24; view: 683; Нарушение авторских прав
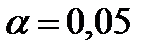 , что в среднем дела идут одинаково хорошо во всех трех городах?
, что в среднем дела идут одинаково хорошо во всех трех городах?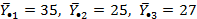 и общее среднее
и общее среднее  .
.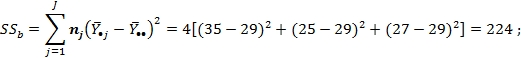

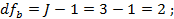

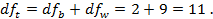
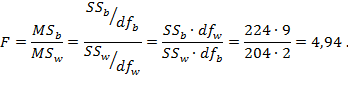
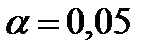
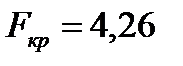 . Следовательно,
. Следовательно,