
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Тригонометрическая и показательная формы комплексного числа
|
|
Рассмотрим полярную систему координат на плоскости, совместив полюс с началом координат, а полярную ось направив по оси OX. Тогда комплексному числу 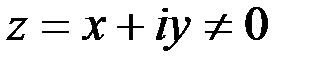 будут соответствовать полярные координаты
будут соответствовать полярные координаты 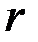 и
и 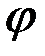 . Число
. Число 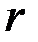 называют модулем комплексного числа:
называют модулем комплексного числа:
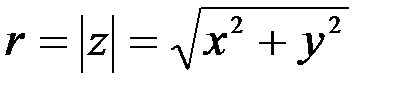 .
.
Геометрический смысл модуля комплексного числа – длина вектора, изображающего комплексное число (рис. 1). Полярную координату 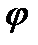 называют аргументом комплексного числа:
называют аргументом комплексного числа:

При этом угол 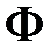 – это угол между вектором, изображающим комплексное число и положительным направлением оси OX (рис. 1). Аргумент комплексного числа
– это угол между вектором, изображающим комплексное число и положительным направлением оси OX (рис. 1). Аргумент комплексного числа  многозначен и определяется с точностью до значения, кратного числу
многозначен и определяется с точностью до значения, кратного числу 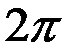 . Главным значением аргумента
. Главным значением аргумента  называют угол, удовлетворяющий условиям
называют угол, удовлетворяющий условиям 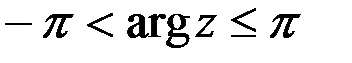 .
.
Тогда 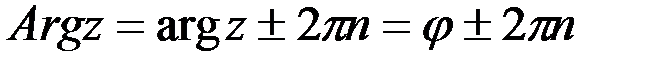 .
.
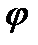 следует учитывать, какой четверти комплексной плоскости соответствует комплексное число:
следует учитывать, какой четверти комплексной плоскости соответствует комплексное число:
Пример 3.  .
.
Число 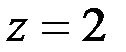 является действительным.
является действительным.
Поэтому  ;
; 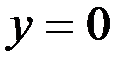
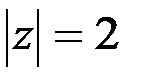 ;
; 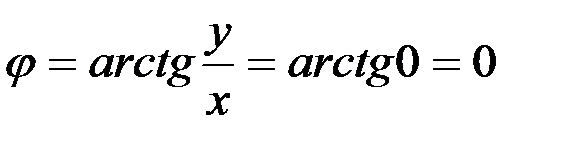 .
.
Пример 4.  .
.
Число  является действительным.
является действительным.
Поэтому 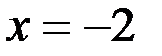 ;
; 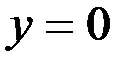
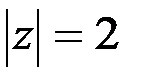 ;
; 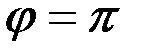 .
.
Такое значение аргумента 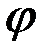 соответствует любому действительному отрицательному числу.
соответствует любому действительному отрицательному числу.
Пример 5.  .
.
Число 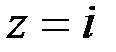 чисто мнимое
чисто мнимое  , а
, а 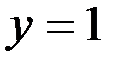 .
.
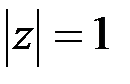 ;
; 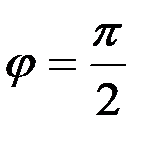 .
.
Такой аргумент соответствует всем чисто мнимым числам  при условии
при условии 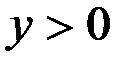 .
.
Пример 6. 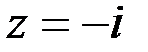 .
.
Это также чисто мнимое число. 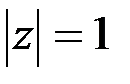 , но
, но  , так как вектор соответствующий комплексному числу направлен вдоль оси OY в отрицательную сторону.
, так как вектор соответствующий комплексному числу направлен вдоль оси OY в отрицательную сторону.
Пример 7. 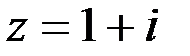 .
.
Здесь 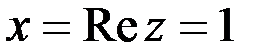 ;
; 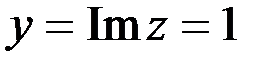
 ;
;  .
.
Пример 8. 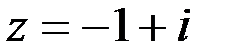 .
.
Здесь  ;
; 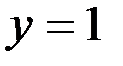 . Вектор, изображающий число, лежит во второй четверти. Поэтому
. Вектор, изображающий число, лежит во второй четверти. Поэтому  .
. 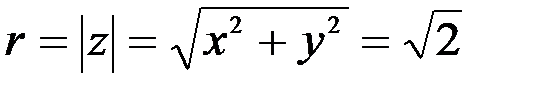 .
.
Пример 9. 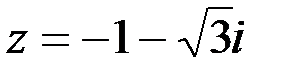 .
.
Здесь 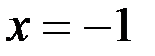 ;
; 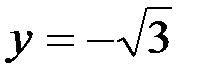
 ;
; 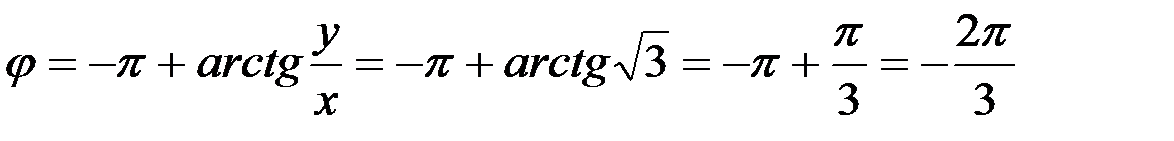
Понятие модуля и аргумента комплексного числа позволяют представить комплексное число в тригонометрической форме:
 ;
;  ;
;
 .
.
Пример 10. Согласно примерам 9,5, 7 получаем:
 ;
;
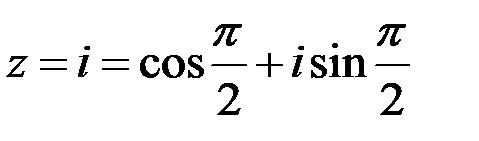 ;
;
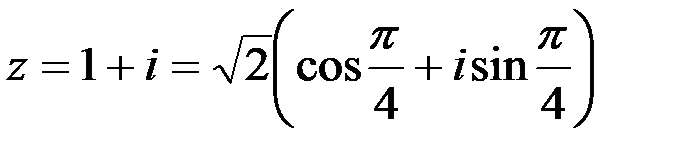 .
.
Разложение стандартной экспоненты в ряд Маклорена позволяет определить показательную функцию с мнимым показателем:
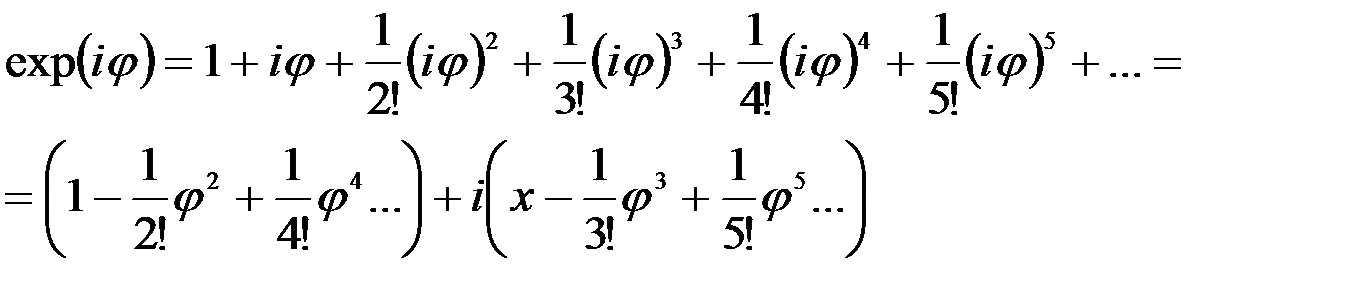
С учетом разложения в ряд функций 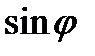 ,
,  :
:
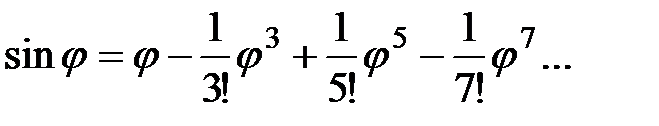 ;
;
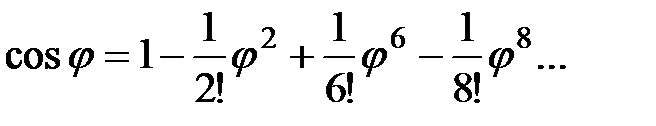 ;
;
получаем формулу Эйлера
 .
.
Формула Эйлера позволяет записать комплексное число в показательной форме
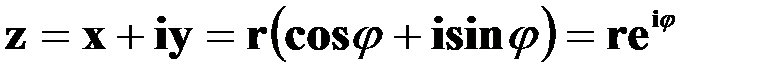 .
.
Пример 11. Продолжая примеры 9,5,7 можно записать числа в показательной форме
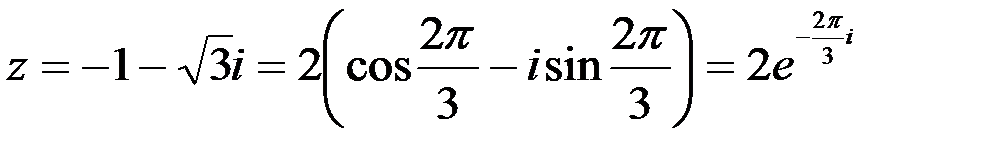 ;
;
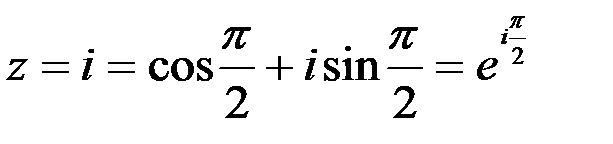 ;
;
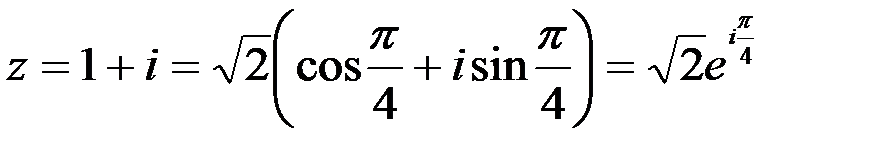 .
.
Запись комплексного числа в показательной и тригонометрической формах очень удобна для выполнения операций умножения, деления, возведения в степень и извлечения корня.
Пусть заданы комплексные числа:
 и
и 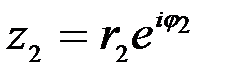 .
.
Тогда справедливо:
1) 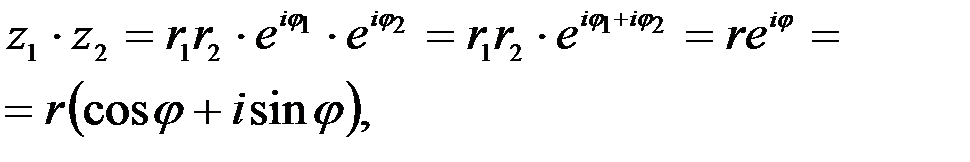
где 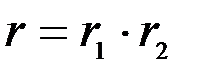 ;
; 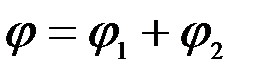 .
.
2) 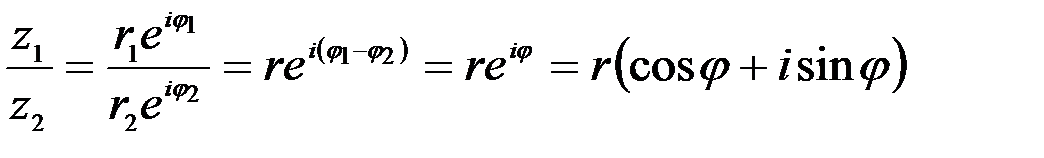 ,
,
где  ;
; 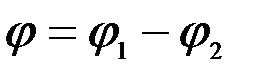 .
.
3) 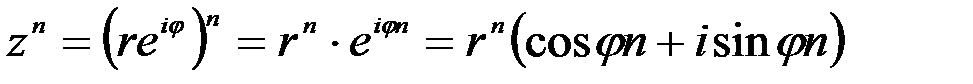 .
.
4) 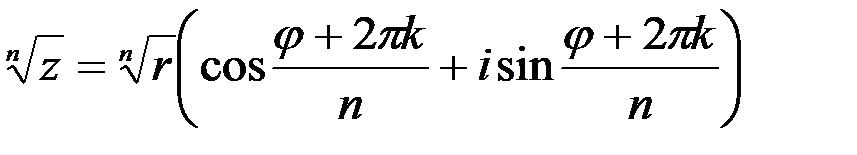 .
. 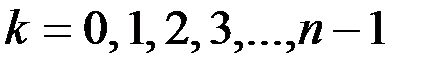 .
.
Заметим, что корни из комплексного числа лежат в вершинах правильного  -угольника, вписанного в круг радиуса
-угольника, вписанного в круг радиуса 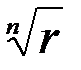 .
.
Пример 12. Выполним действия 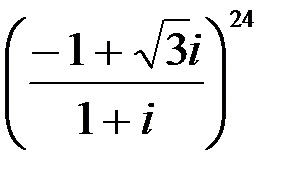 .
.
С учетом того, что 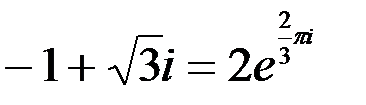 ,
,  , получаем
, получаем
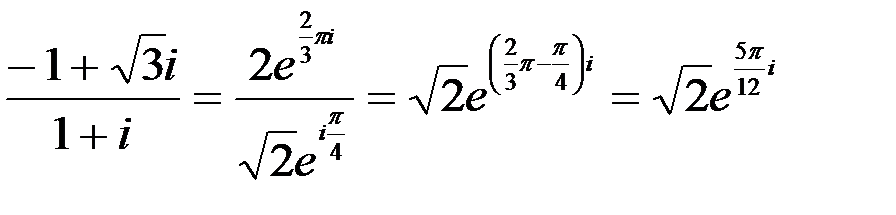 .
.
Далее
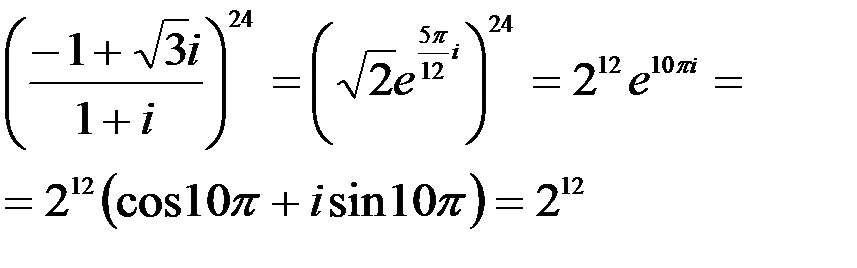
Пример 13. Найдем все корни 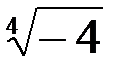 .
.
Число 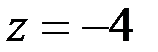 имеет
имеет  и аргумент
и аргумент 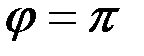 .
.
С учетом этого, все корни можно найти по формуле
 ;
;
 .
.
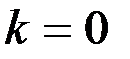 ,
, 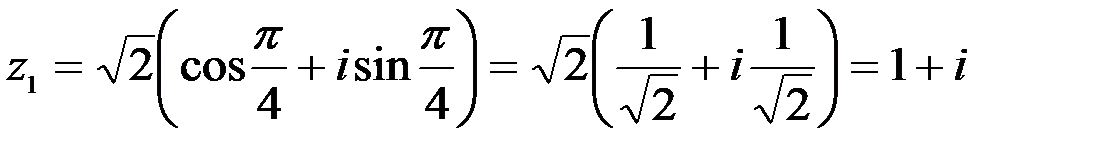 ;
;
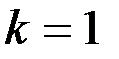 ,
, 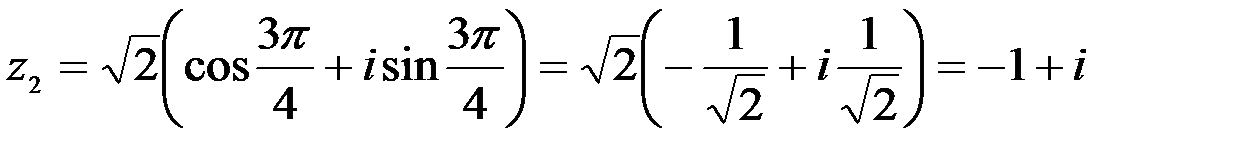 ;
;
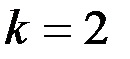 ,
, 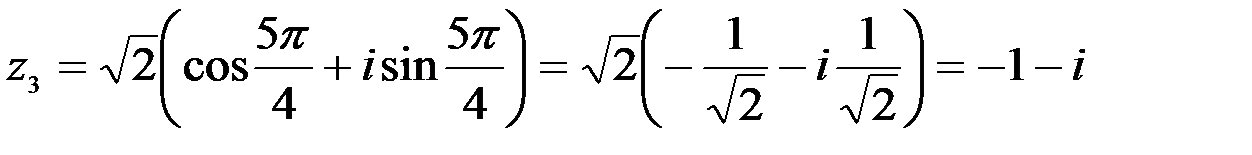 ;
;
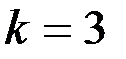 ,
, 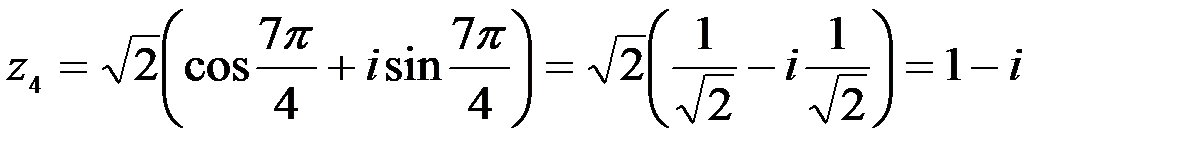 .
.
Расположение корней на комплексной плоскости показано на рис. 4.

|
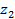
|
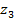
|
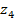
|

|
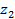
|
| x |
|
| x |
|
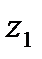
|
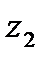
|
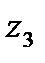
|
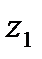
|
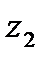
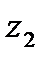
|
Пример 14. Найдем 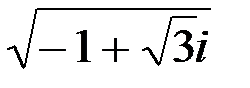 .
.
С учетом того, что  , а аргумент
, а аргумент 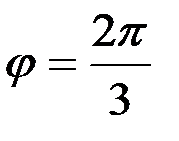 , получаем (рис. 5)
, получаем (рис. 5)
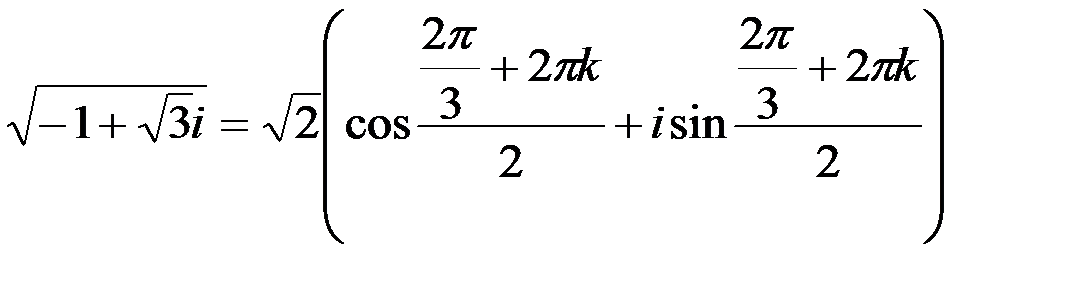 ,
,
 .
.
 ,
, 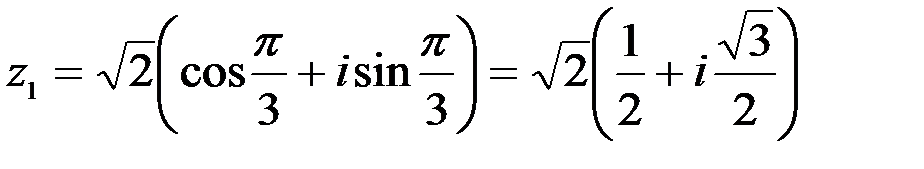 ;
;
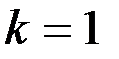 ,
, 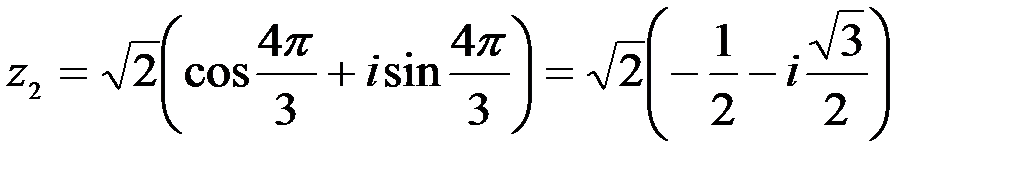 .
.
ЗАДАЧИ
1. Провести вычисления в алгебраической форме:

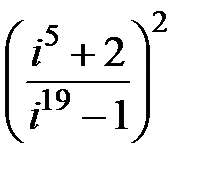
2. Для указанных комплексных чисел определите реальную часть, мнимую часть, модуль и аргумент. Построить вектор комплексного числа на плоскости. Записать число в тригонометрической и показательной формах:
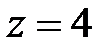

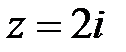

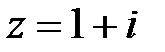
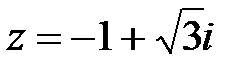
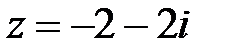
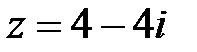
3. Проведите вычисления, используя показательную и тригонометрическую форму записи комплексного числа. Дайте геометрическую интерпретацию операции извлечения корня:
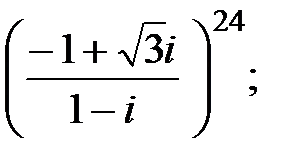
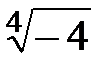 ;
; 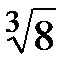 ;
; 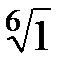 ;
; 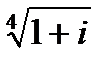
4. Найдите корни уравнений:
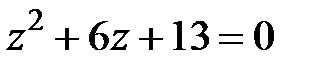 ;
; 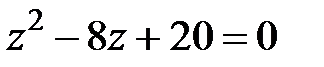 ;
; 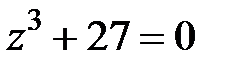 ;
;
Date: 2015-09-24; view: 717; Нарушение авторских прав