Функции комплексной переменной

Понятие функции комплексной переменной. Если каждому комплексному числу 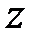, принадлежащему области 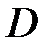(связное открытое множество), поставлено в соответствие некоторое комплексное число 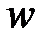, то говорят, что в области 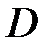определена функция комплексной переменной 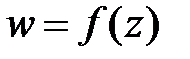, которая может быть представлена с помощью двух действительных функций и 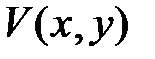действительных аргументов:

,

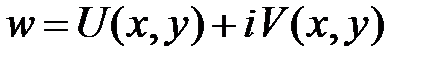где .

К основным элементарным функциям относят:

· Степенную функцию ;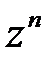

· Показательную функцию ;

· Тригонометрические функции ;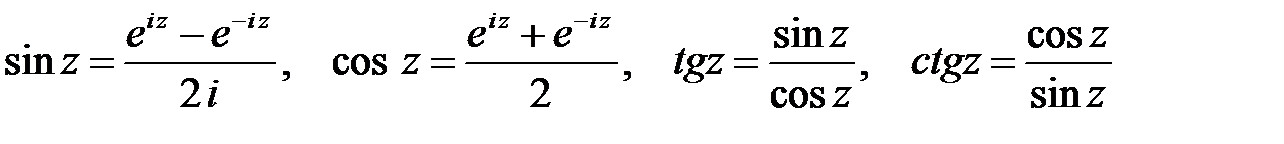

· Гиперболические функции

;

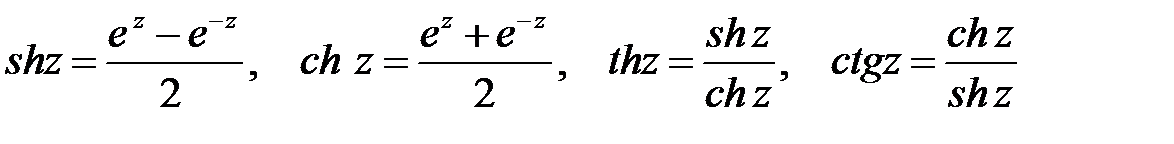· Логарифмическая функция 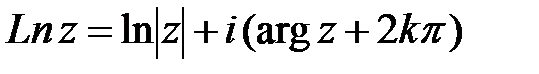является многозначной. В каждой точке 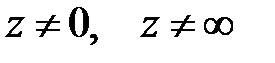она принимает бесконечно много значений. Выражение 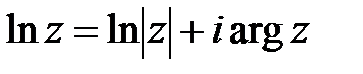называют главным значением логарифмической функции;

· Общая степенная функция 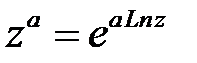является многозначной. В частном случае получаем многозначную функцию – корень 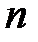-й степени из комплексного числа: .

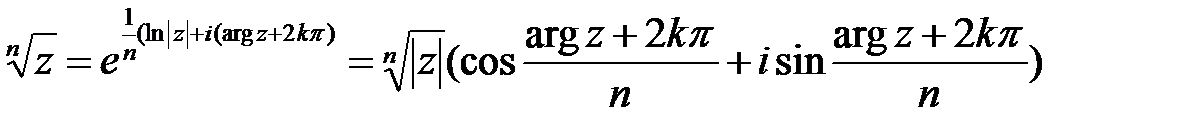· Общая показательная функция 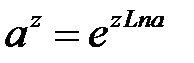является многозначной;

· Обратные тригонометрические и гиперболические функции выражаются через логарифмическую функцию и являются многозначными .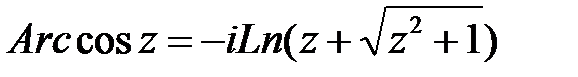

Интеграл от функции комплексной переменной вводится аналогично интегралу от векторной функции вдоль кусочно-гладкой кривой:

.

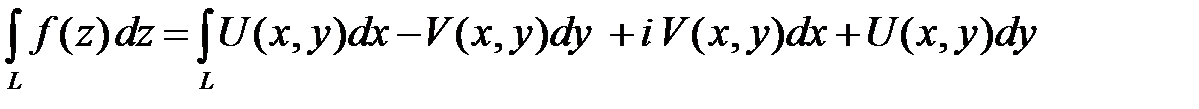Функция 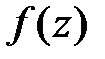, дифференцируемая в некоторой области, и имеющая в этой области непрерывную производную , называется аналитической в этой области. Необходимые и достаточные условия аналитичности в некоторой области выражаются следующими соотношениями:

· Существование непрерывных частных производных функций 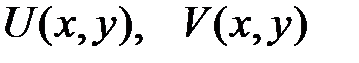, которые удовлетворяют условиям Коши-Римана: ;

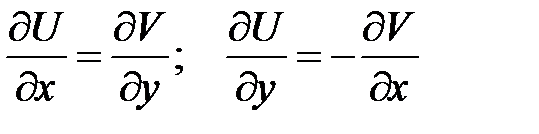· Интеграл по кривой не зависит от контура интегрирования, и справедлива формула Ньютона-Лейбница:

· Интеграл от аналитической функции по замкнутому контуру, который ограничивает односвязную область, равен нулю (теорема Коши для односвязной области):

;

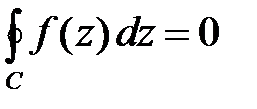· Теорема Коши для многосвязной области:

;

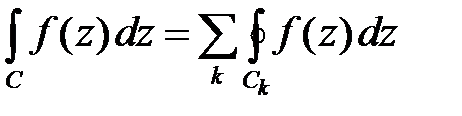· Если функция 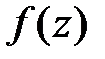аналитична в некоторой области , а контур принадлежит этой области и охватывает точку 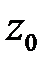, то справедлива интегральная формула Коши, которая связывает значение функции в точке с интегралом по контуру:

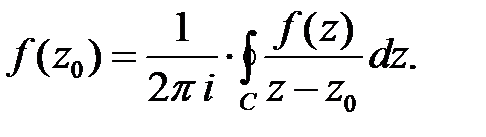
При этом функция 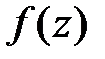имеет в области производные, для которых справедливы формулы:

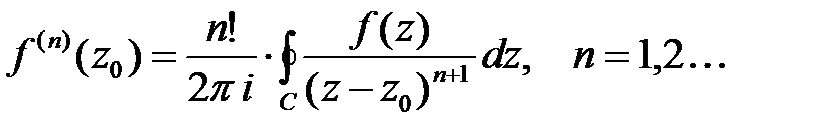
· В окрестности точки аналитичности 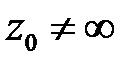функция 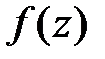представляется рядом Тейлора

,

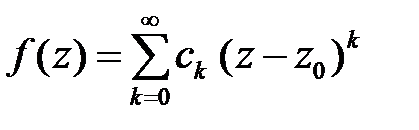областью сходимости которого является круг , радиус

которого равен расстоянию от точки аналитичности до ближайшей особой точки.

· В окрестности особой точки 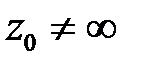функция 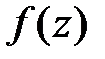представляется рядом Лорана:

,

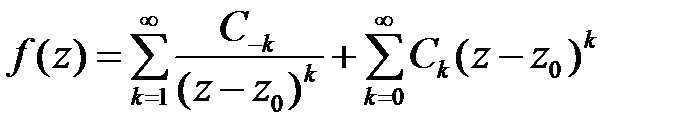который состоит из главной (по отрицательным степеням) и правильной (по положительным степеням) частей. При этом

областью сходимости является кольцо .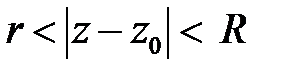

Точка 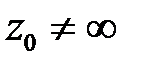называется изолированной особой точкой функции 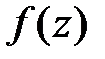, если однозначная функция аналитична в открытом круге . Основой для классификации особых точек является вид разложения в ряд Лорана в окрестности точки:

· Устранимая особая точка – ряд содержит только правильную часть (предел в точке существует и конечен)

;

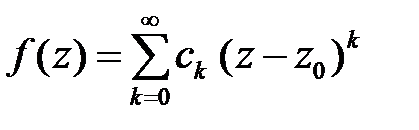· Существенно особая точка – ряд содержит бесконечное число членов в главной части (предел в точке не существует)

;

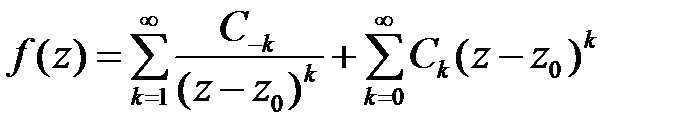· Полюс порядка - ряд содержит конечное число членов в главной части, равное , в главной части (в точке существует бесконечный предел).

Вычетом функции в изолированной особой точке 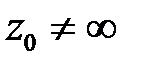называют коэффициент 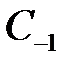при 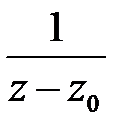разложения в ряд Лорана в окрестности этой точки: 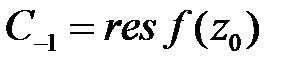. С другой стороны вычет выражается через контурный интеграл

.

Вычет в устранимой особой точке равен нулю. Вычет в существенно особой точке находят непосредственно как коэффициент разложения в ряд. В особой точке типа полюс вычет может быть найден как непосредственным разложением в ряд, так и специально полученных формул:

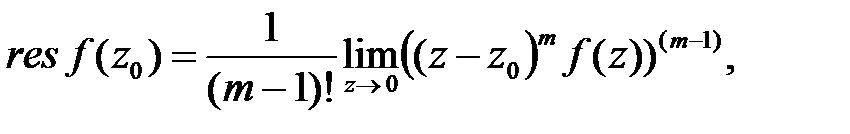
Кроме того для полюса порядка справедлива формула:

.

Вычетом функции 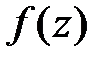в точке 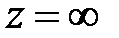называют число , которое является коэффициентом при ряда Лоярана в окрестности бесконечно удаленной точки:

,

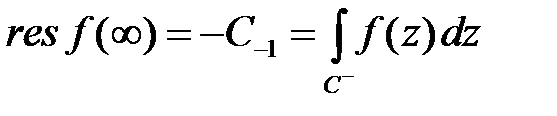где 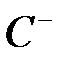- произвольный замкнутый контур, ориентированный по часовой стрелке и принадлежащий области аналитичности функции ().

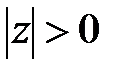Date: 2015-09-24; view: 520; Нарушение авторских прав