Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Преобразования Фурье
|
|
Рассмотрим функцию 
, удовлетворяющую следующим условиям: 1) 
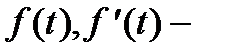определены на интервале 
являются непрерывными или кусочно-непрерывными (могут иметь конечное число точек разрыва 1-ого рода);
2) 
является абсолютно интегрируемой, то есть несобственный интеграл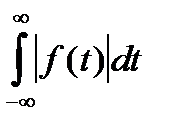 
сходится.
Такая функция может представлена интегралом Фурье:
Внутренний интеграл называют прямым преобразованием Фурье
,
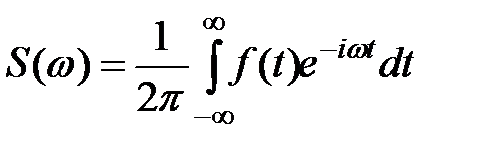а интеграл
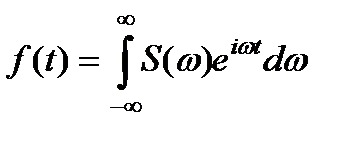
называют обратным преобразованием Фурье.
Прямое преобразование Фурье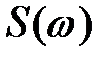 
называют также спектральной плотностью. Эта функция дает анализ частотного состава временного сигнала . В отличие от спектральной плотности периодической функции функция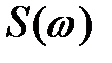 
является непрерывной и служит огибающей для соответствующего дискретного спектра.
Пример 2. Найти спектральную плотность одиночного прямоугольного импульса (рис. 2):
| l/2 |
| l/2 |
| 1 |
| t |
| f(t) |
| Рис. 2 |
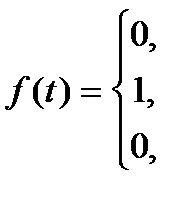
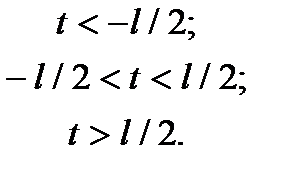
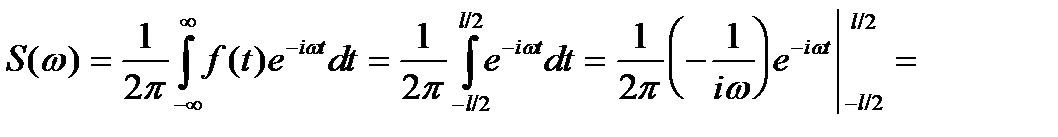
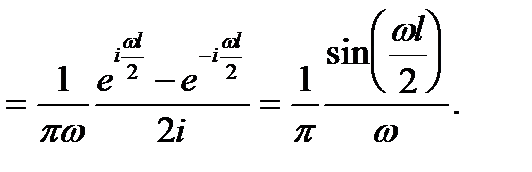
| 0 2p/l w |
| Рис. 3 |
| -2p/l |
 /2p
|
| |S(w)| |
График функции |S(w)| огибает дискретный спектр частот прямоугольного периодического импульса (рис. 3):
Date: 2015-09-24; view: 506; Нарушение авторских прав