Собственные значения и собственные векторы

Собственным вектором линейного оператора (матрицы)

,

соответствующим собственному значению 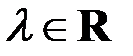называется ненулевой вектор такой, что

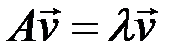. (6.2)

Таким образом, линейный оператор преобразует свой собственный вектор 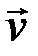в вектор ему коллинеарный (сонаправленный с 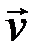при 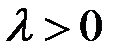и противоположно направленный при 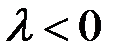). Любой ненулевой вектор 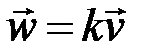, коллинеарный собственному вектору 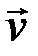, также является собственным, соответствующим тому же собственному значению :

.

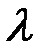В координатах равенство (6.2) имеет вид

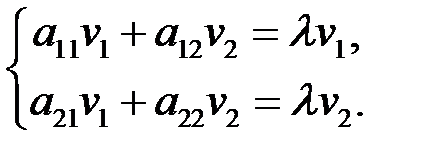
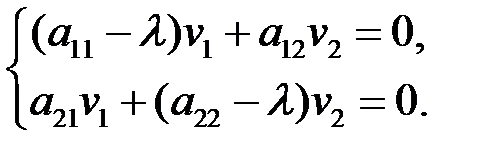(6.3)

Это система линейных уравнений относительно координат 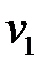, 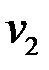собственного вектора. Она имеет ненулевое решение, если определитель системы равен нулю:

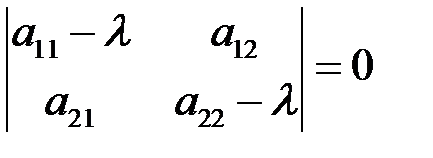
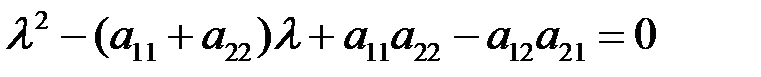. (6.4)

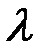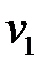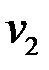Таким образом, для нахождения собственных значений получили квадратное уравнение (6.4). Оно называется характеристическим уравнением. Найдя из него собственное значение , надо подставить его в (6.3). Решив полученную систему линейных уравнений, найдем координаты и собственного вектора, соответствующего собственному значению .

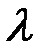Если характеристическое уравнение не имеет действительных корней, то линейный оператор не имеет собственных векторов. Например, их нет у оператора поворота на угол , .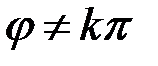

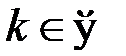Аналогично, формула (6.2) определяет собственный вектор 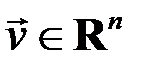, соответствующий собственному значению 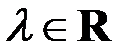, для квадратной матрицы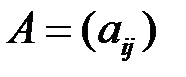 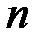-го порядка (линейного оператора в 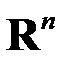) при любом 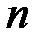. Собственные значения находятся из характеристического уравнения

.

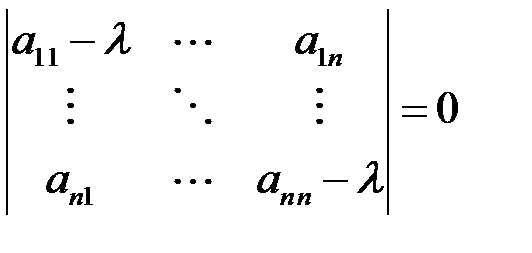
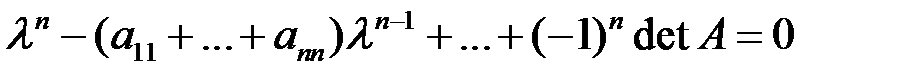Для каждого собственного значения 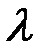координаты 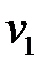,…, 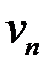соответствующего собственного вектора 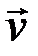находятся из системы линейных уравнений

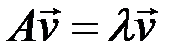
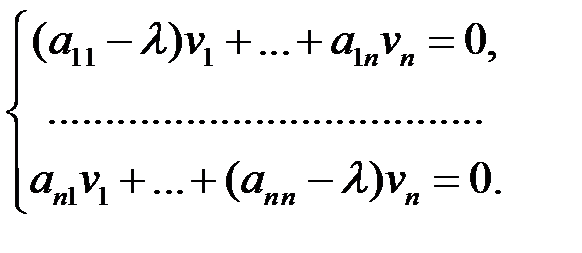
Date: 2015-09-18; view: 470; Нарушение авторских прав