Формула Сомильяны

Итальянский геодезист Сомильяна (Somigliana) в 1929 году получил точную формулу, показывающую распределение силы тяжести на уровенной поверхности эллипсоида вращения. Вопреки правилам русского языка эта формулa вошла в русскую литературу как формула Сомильяна, как если бы его фамилия была Сомильян. Мы будем склонять его фамилию, поэтому должны назвать его формулу именем Сомильяны.

Как мы видели, потенциал притяжения эллипсоида в эллипсоидальных координатах имеет вид (формула (6.17)):

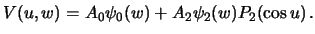
Потенциал тяжести отличается тем, что аддитивно включает в себя центробежный потенциал

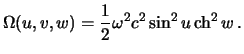
Таким образом

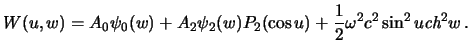
(7.1)

Учитывая, что 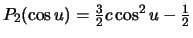, получим

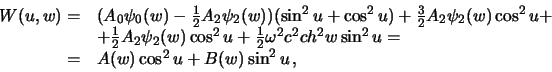
где обозначено

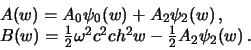
Для того, чтобы получить силу тяжести на поверхности эллипсоида 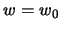, необходимо продифференцировать функцию 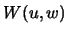вдоль координатной линии 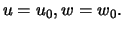Элемент дуги в этом случае равен 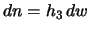, где 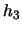-- коэффициент Ламе, который, в данном случае, равен

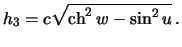
Таким образом, производную потенциала тяжести по нормали к поверхности эллипсоида 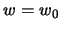можно записать так

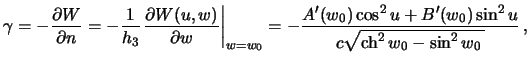
где

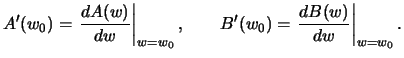
Очевидно, чт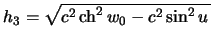о , но 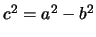, , 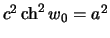поэтому

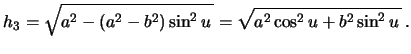
Теперь удельную силу тяжести на поверхности эллипсоида можно записать так

(7.2)

Мы получили искомую формулу для удельной силы тяжести на поверхности уровенного эллипсоида. Однако нам необходимо избавиться от постоянных 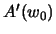и 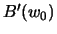. Заметим, что точка 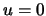, 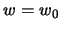соответствует полюсу эллипсоида, а точка 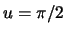, 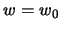-- экватору. Будем снабжать обозначение для силы тяжести соответственно индексами 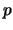и е. Из (7.2) получим

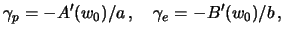
то есть

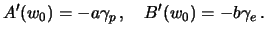
Теперь формулу (7.2) можно переписать следующим образом

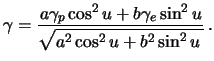
(7.3)

Для того, чтобы получить формулу Сомильяны в окончательном виде, необходимо от эллипсоидальной системы координат перейти к геодезической. Сопоставим две системы координат для точек поверхности эллипсоида

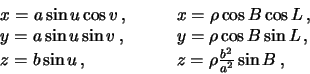
где 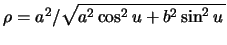(см. лекцию 2, раздел 2.4).

Поскольку (понятия долготы в геодезической и эллипсоидальной системах координат совпадают), поэтому

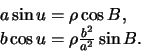
Отсюда

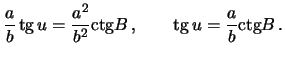
Имеем очевидные выражения для связ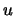и и :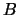

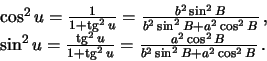
После несложных упрощений, окончательно получим формулу Сомильяны

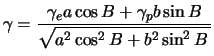
(7.4)

Date: 2015-09-05; view: 1848; Нарушение авторских прав