Гравитационный потенциал эллипсоида вращения

Рассмотрим случай, когда уровенная поверхность есть эллипсоид вращения. Уравнение этой поверхности в декартовых координатах имеет вид

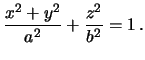
Перейдем к гиперболической системе координат (см. лекцию 2, раздел 2.4)

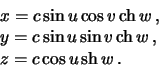
Как мы видели, уравнение эллипсоида вращения с полуосями 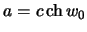, 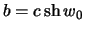имеет вид 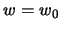. Для определения потенциала притяжения на поверхности уровенного эллипсоида

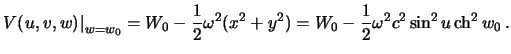
Итак, нам известен потенциал притяжения на поверхности эллипсоида. Требуется определить его во всем внешнем пространстве. Поскольку потенциал притяжения -- гармоническая функция, она подчиняется дифференциальному уравнению Лапласа, которое можно написать в виде

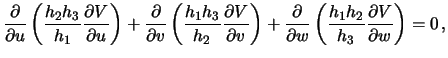
где 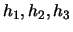-- коэффициенты Ламе. Определим их

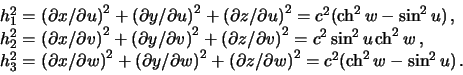
(6.8)

Вычислим отношения коэффициентов Ламе, стоящие в дифференциальном уравнении Лапласа

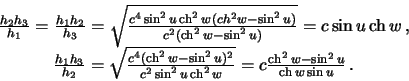
(6.9)

Итак, уравнение Лапласа для функции 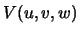принимает вид

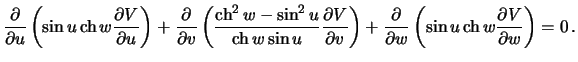
(6.10)

Полученное дифференциальное уравнение линейно, поэтому будем искать решение в виде суммы гармонических функций. В силу осевой симметрии эллипсоида вращения и того, что граничные условия не зависят от переменной 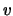-- аналога долготы, то и решение уравнения не должно содержать этой переменной. Иными словами ищем решение в виде

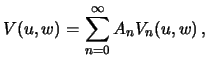
где 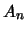-- постоянные, которые нужно определить из краевых условий, а 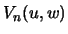-- гармонические функции, удовлетворяющие уравнению Лапласа

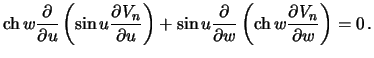
(6.11)

Как и в случае решения дифференциального уравнения для сферических функций, будем искать решение в виде произведения двух функций, каждая из которых является функцией одной переменной

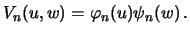
(6.12)

Подставим решение, заданное в виде (6.12) в уравнение (6.11) и поделим полученное уравнение на :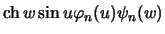

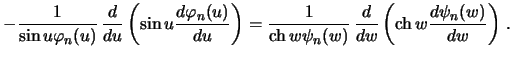
Полученное уравнение справедливо при любых значениях независимых переменных. Это возможно лишь в том случае, когда обе части этого уравнения равны одной и той же постоянной. Обозначим эту постоянную через 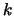. Получим два дифференциальных уравнения

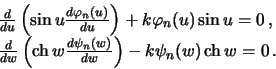
(6.13)

Покажем, что первое из приведенных здесь уравнений при 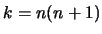есть уравнение для полиномов Лежандра (см. лекцию 3, уравнения (3.24)-(3.26)), то есть

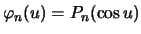
(6.14)

Положим 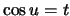, , 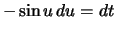тогда вместо первого из уравнений (6.13) будем иметь

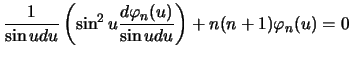
или

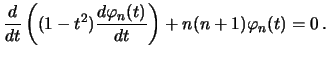
(6.15)

Уравнение (6.15) совпадает с уравнением для полиномов Лежандра (см. лекцию 3, формула (3.24))

Итак, решением уравнения Лапласа в гиперболической системе координат будет функция

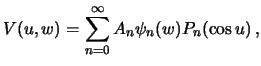
(6.16)

которая на поверхности эллипсоида принимает значения

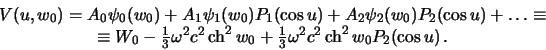
(6.17)

При выводе формулы (6.17) мы приняли во внимание, что 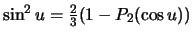. Сравнивая левую и правую части формулы (6.17) мы приходим к выводу, что

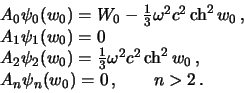
(6.18)

Итак, в формуле (6.16) для потенциала притяжения эллипсоида отличные от нуля только коэффициенты 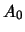и 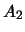, поэтому строгое выражение для потенциала в гиперболических координатах можно записать в виде

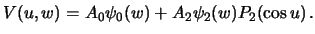
(6.19)

Остается определить функции и 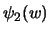. Как следует из уравнений (6.13), функцию 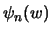можно определить, решив второе из названных уравнений 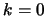при и при :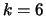

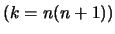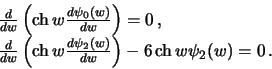
(6.20)

Полученным дифференциальным уравнениям удовлетворяют функции

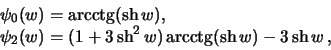
в чем можно убедится простой подстановкой в уравнения (6.20).

Избавимся теперь от гиперболических функций, полученных нами при решении дифференциальных уравнений. Как мы уже говорили, переменная 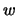определяет семейство софокусных эллипсоидов. Возьмем некоторую точку на оси вращения эллипсоида, находящуюся на расстоянии 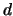от центра. Тогда для этой точки 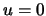, 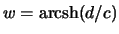. Заменим переменную 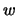на :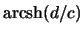

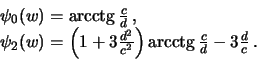
(6.21)

Итак, потенциал притяжения в произвольной точке вне эллипсоида имеет вид

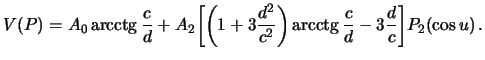
(6.22)

Коэффициенты 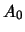и 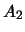определим из краевого условия

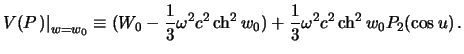
Заметим, что 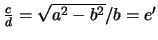, , 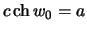после соответствующих преобразований получим

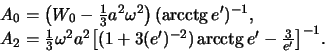
(6.23)

Формулы (6.22) и (6.23) определяют потенциал притяжения эллипсоидальным телом материальной точки, лежащей на поверхности софокусного эллипсоида

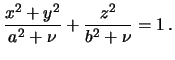
Зная координаты точки 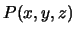и полуоси эллипсоида 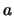и 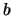легко определить параметр 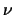, а следовательно и малую полуось 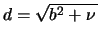эллипсоида, проходящего через заданную точку.

Из приведенных формул видно, что потенциал притяжения содержит лишь четыре независимых параметра 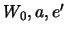и 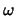. Эти четыре параметра абсолютно строго определяют потенциал притяжения эллипсоидальным телом материальной точки, лежащей во вешнем пространстве, при любом распределении масс внутри тела лишь бы его поверхность оставалась поверхностью уровня.

Date: 2015-09-05; view: 748; Нарушение авторских прав