
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Приклади та завдання
|
|
Приклад 7. Визначити способом найменших квадратів параметри А і В залежності: Δ=А+В·RZ.
Значення величин представлені в таблиці 1.
Таблиця 1
| i | RZ,мкм | Δ | i | RZ,мкм | Δ |
| 0,072 | 2,8 | 0,140 | 3,0 | ||
| 0,080 | 2,6 | 0,140 | 3,4 | ||
| 0,112 | 3,2 | 0,183 | 3,7 | ||
| 0,120 | 2,9 | 0,208 | 4,1 | ||
| 0,130 | 3,1 | 0,241 | 4,5 | ||
| 0,136 | 3,4 | 0,268 | 4,8 |
Систему рівнянь одержуємо підстановкою табличних даних в рівняння залежності:
А+В·(Rz)i=Δi, і=1,2,……12.
Таким чином, число (n) рівнянь дорівнює дванадцяти, число (m) невідоме двом (А і В). В позначеннях Гаусса система нормальних рівнянь має вигляд:
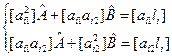
де А і В - оцінки параметрів, що відшукуються аі1=1, аі2=(Rz)і, li=Δi.
Приклади обчислення коефіцієнтів у системі наведені в таблиці 2.
Таким чином, 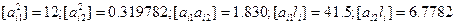
Для системи нормальних рівнянь одержуємо:
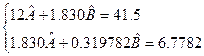
Таблиця 2
| i | 
| 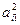
| 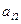
| 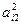
| 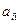 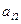
| 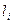
| 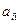 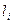
| 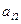 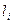
|
| 0,072 | 0,005184 | 0,072 | 2,8 | 2,8 | 0,2016 | |||
| 0,080 | 0,006400 | 0,080 | 2,6 | 2,6 | 0,2080 | |||
| 0,112 | 0,012544 | 0,112 | 3,2 | 3,2 | 0,3584 | |||
| 0,120 | 0,014400 | 0,120 | 2,9 | 2,9 | 0,3480 | |||
| 0,130 | 0,016900 | 0,130 | 3,1 | 3,1 | 0,4030 | |||
| 0,136 | 0,018496 | 0,136 | 3,4 | 3,4 | 0,2624 | |||
| 0,140 | 0,019600 | 0,140 | 3,0 | 3,0 | 0,4200 | |||
| 0,140 | 0,019600 | 0,140 | 3,4 | 3,4 | 0,4760 | |||
| 0,183 | 0,033489 | 0,183 | 3,7 | 3,7 | 0,6771 | |||
| 0,208 | 0,043264 | 0,208 | 4,1 | 4,1 | 0,8528 | |||
| 0,241 | 0,058081 | 0,241 | 4,5 | 4,5 | 1,0845 | |||
| 0,268 | 0,071824 | 0,268 | 4,8 | 4,8 | 1,2864 | |||
| Суми | 0,319782 | 1,830 | 41,5 | 6,7782 |
звідки знаходимо оцінки 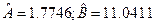
В загальному вигляді вирішення системи нормальних рівнянь запишемо
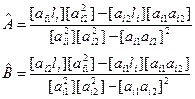
Можна переписати так 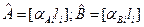
Де 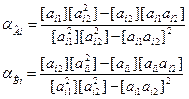
Визначення цих коефіцієнтів зручно обчислювати, як показано в таблицях 3, 4, 5.
Тепер за формулою 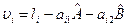 можна обчислити остаточні похибки, їх квадрати і суму квадратів.
можна обчислити остаточні похибки, їх квадрати і суму квадратів.
Оцінка для дисперсії похибок складає
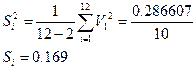
Знаходимо оцінки середнього квадратичного відхилення результатів сумісних вимірів параметрів А і В залежності
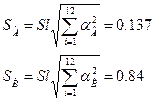
Таблиця 3
| i | 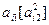
| 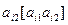
| 2-3 | 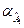
| 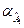
|
| 0.319782 | 0.13176 | 0.188022 | 0.385 | 0.148225 | |
| 0.319782 | 0.14640 | 0.173382 | 0.355 | 0.126025 | |
| 0.319782 | 0.20496 | 0.114822 | 0.236 | 0.055696 | |
| 0.319782 | 0.21960 | 0.100182 | 0.205 | 0.042025 | |
| 0.319782 | 0.23790 | 0.081882 | 0.168 | 0.028224 | |
| 0.319782 | 0.24888 | 0.070902 | 0.145 | 0.021025 | |
| 0.319782 | 0.25620 | 0.063582 | 0.130 | 0.016900 | |
| 0.319782 | 0.25620 | 0.063582 | 0.130 | 0.016900 | |
| 0.319782 | 0.33489 | -0.015108 | -0.031 | 0.000961 | |
| 0.319782 | 0.38064 | -0.060858 | -0.125 | 0.015625 | |
| 0.319782 | 0.44103 | -0.121248 | -0.248 | 0.061504 | |
| 0.319782 | 0.49044 | -0.170658 | -0.350 | 0.122500 | |
| Сума | 0.655610 |
Таблиця 4
| i | 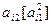
| 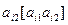
| 2-3 | 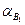
| 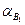
|
| 0,864 | 1,830 | -0,966 | -1,980 | 3,920400 | |
| 0,960 | 1,830 | -0,870 | -1,780 | 3,168400 | |
| 1,344 | 1,830 | -0,486 | -0,994 | 0,988036 | |
| 1,440 | 1,830 | -0,390 | -0,799 | 0,638401 | |
| 1,560 | 1,830 | -0,270 | -0,553 | 0,305809 | |
| 1,632 | 1,830 | -0,198 | -0,406 | 0,164836 | |
| 1,680 | 1,830 | -0,150 | -0,307 | 0,094249 | |
| 1,680 | 1,830 | -0,150 | -0,307 | 0,094249 | |
| 2,169 | 1,830 | +0,366 | +0,750 | 0,562500 | |
| 2,496 | 1,830 | +0,666 | +1,365 | 1,863225 | |
| 2,892 | 1,830 | +1,062 | +2,17 | 4,708900 | |
| 3,216 | 1,830 | +1,386 | +2,84 | 8,065600 | |
| Сума | 24,574605 |
Таблиця 5
| i | 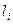
| 
| 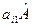
| 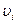
| 
|
| 2,8 | 0,7949 | 1,7746 | -0,2305 | 0,052900 | |
| 2,6 | 0,8832 | 1,7746 | +0,0578 | 0,003340 | |
| 3,2 | 1,2365 | 1,7746 | -0,1889 | 0,035721 | |
| 2,9 | 1,3248 | 1,7746 | +0,1994 | 0,039601 | |
| 3,1 | 1,4352 | 1,7746 | +0,1098 | 0,012100 | |
| 3,4 | 1,5014 | 1,7746 | -0,1240 | 0,015376 | |
| 3,0 | 1,5456 | 1,7746 | +0,3202 | 0,102400 | |
| 3,4 | 1,5456 | 1,7746 | -0,0798 | 0,006400 | |
| 3,7 | 2,0203 | 1,7746 | +0,0949 | 0,009025 | |
| 4,1 | 2,2923 | 1,7746 | -0,0331 | 0,001096 | |
| 4,5 | 2,6606 | 1,7746 | -0,0648 | 0,004199 | |
| 4,8 | 2,9587 | 1,7746 | -0,0667 | 0,004449 | |
| Сума | 0,286607 |
Значення суми квадратів коефіцієнтів 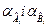 взяті з табл. 3 і 4.
взяті з табл. 3 і 4.
Остаточно результати вимірювань записують в такому вигляді:
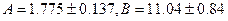
Приклад 8. Досліджується новий цифровий термометр, прототипом якого за попередніми даними може бути серійний термометр типу ТТЦ-2 для контактного вимірювання температури поверхні нагрітих об’єктів до 1000с (методом парної кореляції).
При попередньому дослідженні виявлені основні технічні параметри досліджуваноготермометра, серед яких:
- поріг чутливості – y1;
- роздільна здатність – у2;
- основна похибка – у3;
- нижня межа вимірювань – у4;
- максимальне значення оточуючої температури – у5.
Після проведення попередніх експериментів отримуємо матрицю коефіцієнтів парної кореляції, яка подана в таблиці:
| Параметри отимізації | y1 | y2 | y3 | y4 | y5 |
| Y1 | +0.014 | -0.057 | 0.108 | +0.489 | |
| Y2 | +0.106 | +0.148 | +0.676 | ||
| Y3 | +0.148 | -0.594 | |||
| Y4 | -0.886 | ||||
| Y5 |
У результаті аналізу, проведенного за даними таблиці, можна зробити такий висновок: - від параметра у5 можна відмовитися, а за параметр оптимізації довільно вибрати основну похибку у3 як таку, що легко піддається перевірці з трьох найближчих параметрів у1, у2, у3.
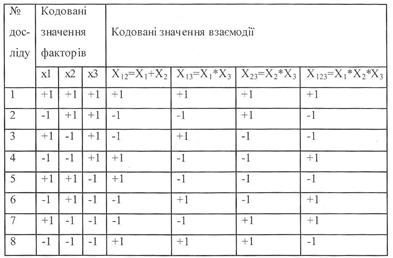
Приклад 9. Побудувати плани розширених (з урахуванням факторів взаємодії) повних факторних експериментів типів 22, 23.
Ці плани типів 22, 23, відповідно, подані у таблиці 1 і 2.
Таблиця 1
| № досліду | Кодові значення факторів | Кодовані значення факторів взаємодії | |
| X1 | X2 | X12=X1*X2 | |
| +1 | +1 | +1 | |
| -1 | +1 | -1 | |
| -1 | -1 | -1 | |
| -1 | -1 | +1 |
Таблиця 2
Приклад 10. Досліджується якість харчового продукту, термін зберігання якого залежить від температури зберігання в діапазоні від 100 до 400С й вологості від 30 до 100%.
Побудуємо матрицю даних табл. 1 і 2.
Таблиця 1
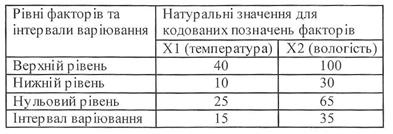
Таблиця 2
| № досліду | Кодовані значення факторів | ||
| X1 | X2 | X1X2 | |
| +1 | +1 | +1 | |
| -1 | +1 | -1 | |
| +1 | -1 | -1 | |
| -1 | -1 | +1 |
Математична модель в кодованих значеннях має такий вигляд:
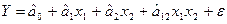
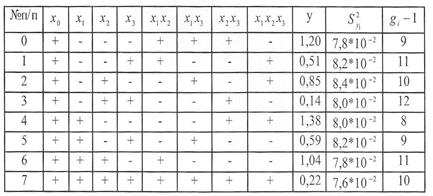
Завдання 1. У результаті проведення ПФЕ одержані результати, які зведені в таблицю:
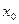
| 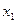
| 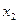
| y | 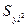
| 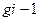
|
| + | - | - | 2.5 | 1.5*10-2 | |
| + | - | + | -0.5 | 3*10-2 | |
| + | + | - | 3.5 | 1*/10-2 | |
| + | + | + | 2.5 | 2.5*10-2 |
Вирішення:
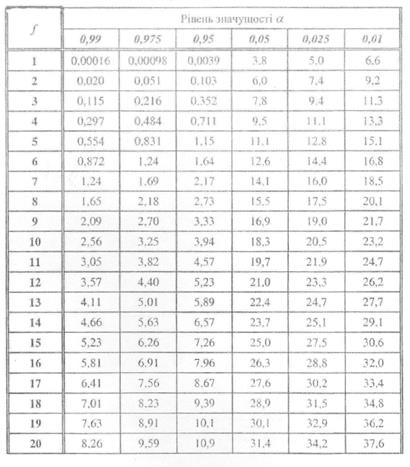
Перш ніж приступити до розрахунку коефіцієнтів рівняння регресії, перевіримо гіпотезу про однорідність дисперсії відтворюваності в точках фактичного простору. Оскільки число повторних дослідів однакове, для перевірки однорідності використаємо критерій Кохрена. Обчислюємо розраховане значення критерія:
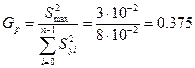
За таблицями значень критерія Кохрена для рівня значущості α=0,05 числа ступені свободи g-1=10 і числа точок факторного простору N=4 знаходимо критичні значення GT1=0,4884,
Оскільки обчислене значення G p <G, гіпотеза про однорідність дисперсії приймається.
Розрахуємо дисперсію відтворюваності експерименту, усереднюючи дисперсії відтворюваності дослідів.
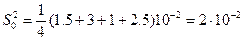
Тепер обчислюємо значення коеффіцієнтів рівняння регресії за формулою
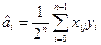
При цьому 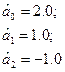
Дисперсія оцінки коеффіцієнтів 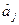 дорівнює:
дорівнює:
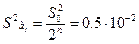
Звідки:. 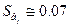
Переходимо до статистичного аналізу результатів обробки ПФЕ. Оцінимо значущість одержаних коефіцієнтів регресії.
Згідно з методикою введемо ймовірну величину:
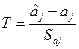
розподілену за законом Ст’юдента:
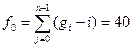
Довірчий інтервал 2εвj для 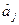 обчислюємо так, щоб
обчислюємо так, щоб
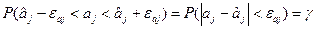
Тепер, задаючись величиною довірчої ймовірності γ (наприклад γ=0,95), за таблицею розподілу Ст ׳юдента для одержаного значення числа ступенів свободи f 0 =40, знайдемо значення tа j для якого
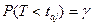
При цьому taj=2.02.
Тоді 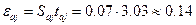
Звідки 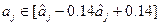
При цьому 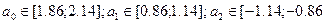
Оскільки не один з обчислених інтервалів не захоплює нуль, всі коефіцієнти рівняння регресії вважаємо значущими.
Тоді функція відклику має вигляд

Оцінимо адекватність одержаної моделі. Розрахуємо дисперсію адекватності:
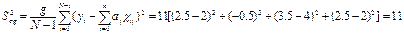
Тоді розраховане значення відношення Фішера
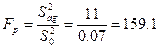
Далі за таблицею розподілу Фішера для рівня значущості α=0,05 число ступенів свободи f ag= N -1 =1 і f N (g-1)=40 знаходимо 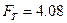 Оскільки
Оскільки 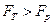 .гіпотезу про адекватність моделі необхідно відкинути.
.гіпотезу про адекватність моделі необхідно відкинути.
Ймовірною причиною неадекватності моделі може бути неврахування взаємодії x1 x2.
Після введення цієї взаємодії в рівняння регресії воно одержує вигляд

Внаслідок однієї наявності матриці планування оцінювання коефіцієнтів рівняння регресії виконуємо незалежно один від одного. Тому
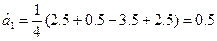
Тепер рівняння регресії запишемо наступним чином:
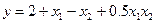
Видно, що при цьому одержані в експерименті й обчислені згідно з рівняння регресії значення співпадають і таким чином скоригована модель адекватна.
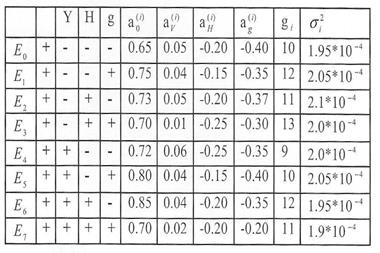
Завдання 2. Для оцінки ефективності передачі даних залежно від бачності передачі - V, середньої частини дубльованої частини повідомлень - H і відношення сигнал/шум - g був проведений ряд експериментів. Обробку їх результатів проводили з використанням штучної ортогоналізації результатів. При цьому оцінки за МНК коефіцієнтів гіперплощин, які
описують поведінку функції в кожній з підобластей ортокермованого три факторного простору, дали такі результати.
Як функцію відклику використовуємо співвідношення
Y=(V.H.g)=-lnP(V.H.g),
де Р(V.H.g) – ймовірність успішної передачі повідомлення для заданих значень V.H.g.
Коваріаційна матриця помилок оцінок коефіцієнтів гіперплощин має вигляд
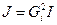
Необхідно описати залежність ймовірності успішної передачі повідомлення від V.H.g, розрахувати ймовірність успішної передачі для найкращих, найгірших середніх умов передачі повідомлень.
Вирішення:
Для опису функції відклику використаємо рівняння регресії
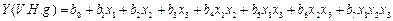
 (7.1)
(7.1)
Оцінювання коефіцієнтів регресії (7.1) проведемо з використанням результатів ПФЕ, що формуються за методом штучної ортогоналізації. Згідно з методом за частковим описом функцій відклику в підобластях Е 0,Е1…Е7 обчислимо оцінки функції відклику в ортогональних точках і відповідні дисперсії:
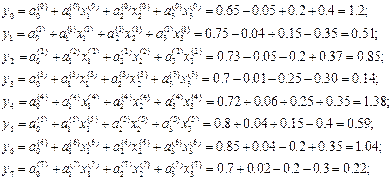
Дисперсії оцінки i y в ортогональних точках знайдемо за формулою
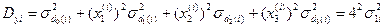
Перевіримо гіпотезу про однорідність дисперсій. Тому що gi 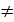 g, використаємо критерії Фішера:
g, використаємо критерії Фішера:
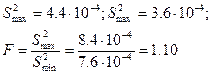
За таблицею розподілу Фішера виберемо Fm, задавши a=0.05, fi1=10 i fi2 =10
При цьому FT=2.98. Оскільки F<F m, то немає підстав для відхилення гіпотези H 0 про те, що дисперсії однорідні.
Обчислимо тепер дисперсію відтворюваності експерименту
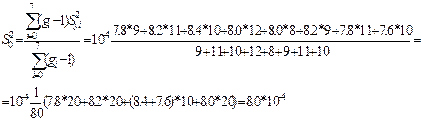
Згідно з методикою обробки результатів ПФЕ маємо:
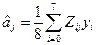 (7.2)
(7.2)
де Z ij - значення j-го фактора в i-му експерименті.
У результаті підрахунку за формулою (7.2) одержимо:
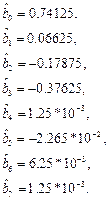
Дисперсії оцінки коефіцієнтів â j визначаються співвідношенням
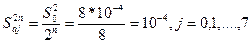
Оцінимо значущість коефіцієнтів функції відклику. Введемо випадкову величину
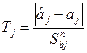
Розподілену за законом Ст ׳юдента з 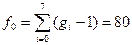 ступенями свободи.
ступенями свободи.
Виберемо тепер величину 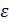 âj так, що
âj так, що 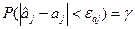
Тоді маємо
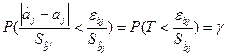
Використаємо таблиці t-розподілу, знаходимо (f0=80, a=1-y=0.05)таке
Число taj=1.99, для якого нерівність 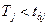 виконується із заданою ймовірністю. Тоді
виконується із заданою ймовірністю. Тоді
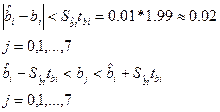
В нашому 
Таким чином, довірчий інтервал, який накриває із заданою ймовірністю (j=0,95) істинне значення коефіцієнта bj рівняння регресії дорівнює
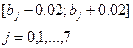
Будемо вважати, що коефіцієнт bj значущий, якщо відповідний довірчий інтервал захоплює нуль, тобто якщо:
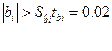
У протилежному разі цей коефіцієнт необхідно визнати
незначним. У розглянутому прикладі коефіцієнт d4, b6 і b7 мають числове значення менше 10-2, тому вважаємо їх незначними.
Таким чином, функція відклику має вигляд y(v,h,q)=0.74125+0.06625x1-0.17875x2-0.37625x3-0.02625x1x3.
Розрахуємо дисперсію адекватності:
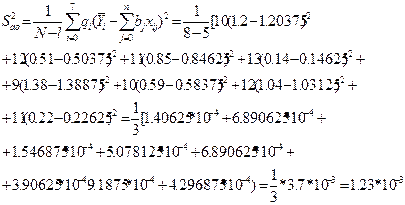
Для оцінки адекватності використаємо критерій Фішера:
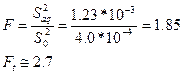 (при рівні значущості α=0,05)
(при рівні значущості α=0,05)
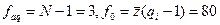
Отже, модель адекватна. При цьому P(v,h,q)=e-y(v,h,q).
Розрахуємо ймовірність успішної передачі для найкращих умов x1=1(vmin), x2=1(Hmax), x3=1(qmax).
Тоді
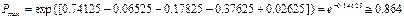
У найгірших умовах передачі: x1=1(vmax), x2=1(Hmin), x3=1(qmin).
Тоді:
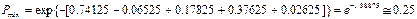
Нарешті для середніх умов передачі повідомлень х1=х2=х3=0
(Vcp, Hcp,qcp).
Тоді: P =exp{-0.74125} 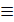 0.477
0.477
Завдання 6. Визначити результатам опосередкованих вимірювань величини Х=0,3Х1 е0,01x2 і границі його похибки для наведених в табл. 1 результатів багатократних вимірювань Хі і Х2. З урахуванням кореляції ними. Довірча ймовірність РД = 0,95.
| X1 | X2 | X3 | X4 |
| 21.582 | 20.585 | 20.683 | 21.749 |
| 21.515 | 20.595 | 20.750 | 21.836 |
| 21.410 | 20.641 | 20.854 | 21.882 |
| 21.279 | 20.724 | 20.986 | 21.881 |
| 21.133 | 20.840 | 21.131 | 21.834 |
| 20.987 | 20.982 | 21.277 | 21.743 |
| 21.855 | 21.143 | 21.409 | 21.615 |
| 21.751 | 21.311 | 21.514 | 21.458 |
| 20.684 | 21.476 | 21.581 | 21.285 |
| 20.660 | 21.625 | 21.605 | 21.108 |
Вирішення:
1. Визначаємо середні арифметичні аргументів рівняння вимірювання:
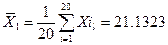
2. Знаходимо оцінки дисперсії результатів спостереження аргументів:
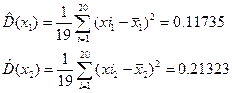
і оцінки дисперсії результатів їх вимірювання:
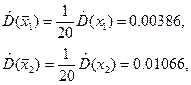
3.Розраховуємо значення коефіцієнтів впливу:
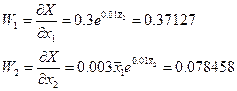
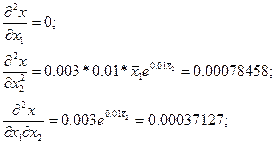
4. Порівнюємо можливість застосування формули для оцінки границь похибки:
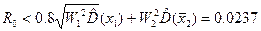
Де 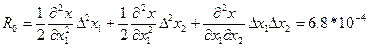
Для 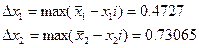
Оскільки нерівність виконується, поляризація можлива.
5. Розраховуємо оцінку кореляційного моменту:
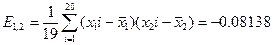
6. Розраховуємо коефіцієнт кореляції:
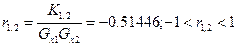
7. Перевіряємо наявність кореляції між х1 і х2 за формулою

де ts знаходимо за таблицею розподілу. Для ймовірності Рд = 0,95 і низкиспостережень n-2=18, ts =2,11.
Оскільки 2,54 > 2,11, тобто нерівність не виконується, то маємо кореляційний зв΄язок х1 і х2.
8. Перевіряємо графічно наявність кореляції між х1 і х2, для чого представимо залежність між х2 і х1 (рис.7.6)
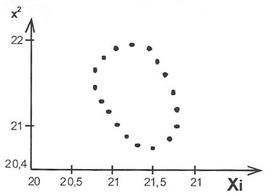
Рис.7.6 - Залежність х2 (х1)
З рисунку видно, що між х1 і х2 е кореляція, причому r1,2<0.
9. Результати вимірювання х розраховуємо за формулою

10. Оцінка дисперсії результатами вимірювань буде дорівнювати
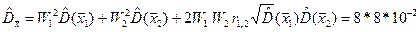
11. Границі випадкової похибки результату опосередкованого вимірювання знаходимо за формулою
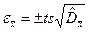 , де ts- коефіцієнт Ст’юдента для ймовірності 0,95 і число ступенів свободи Кеф яке визначаємо за формулою
, де ts- коефіцієнт Ст’юдента для ймовірності 0,95 і число ступенів свободи Кеф яке визначаємо за формулою
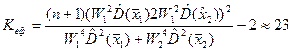
Для ймовірності Рд=0,95 і Кеф 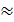 23 знайдемо із таблиці Ст’юдента значення ts=2, тоді
23 знайдемо із таблиці Ст’юдента значення ts=2, тоді
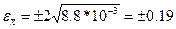
Завдання 7. При дослідженні пускорегулюючого пристрою одержані дані експерименту:
| ti,c | |||||||||||
| Ii,A |
t час і – струм.
Відповідно до теоретичних даних залежність струму від часу має вигляд i=i0e-at, де i0 початкова сила струму, і0=100А; α- шуканий параметр, a=(rb+rp)/Lb
На основі дослідних даних визначаємо в першому наближенні α. Відомо, що функція е-х при х=3 досягає значення 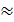 0,05. Тоді, як видно з експерименту, при t=9-10с значення і=0,05 і0 і, таким чином, α приблизно дорівнює 0,3 1/е. Для уточнення α скористаємося методом найменших квадратів. Задаємося кількома значеннями α, близькими до 0,3 1/с.
0,05. Тоді, як видно з експерименту, при t=9-10с значення і=0,05 і0 і, таким чином, α приблизно дорівнює 0,3 1/е. Для уточнення α скористаємося методом найменших квадратів. Задаємося кількома значеннями α, близькими до 0,3 1/с.
Потім за формулою обчислюємо сили струму іі в точках t=ti. Згідно з цим обчислюємо значення суми квадратів відхилень
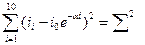 для різних α.
для різних α.
Оформляємо результати обчислень:
| α 1/c | 0.28 | 0.29 | 0.30 | 0.31 | 0.32 | 0.33 |
 A2 A2
| 83.3 | 40.3 | 17.4 | 13.6 | 25.7 | 51.4 |
Будуємо графік функції  (рис.7.7), знайдемо, що
(рис.7.7), знайдемо, що  при α=0,307.
при α=0,307.
Отже, найкращим наближення до дослідних даних є функція 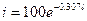 Графік цієї функції і експериментальні точки показані на рис.7.8.
Графік цієї функції і експериментальні точки показані на рис.7.8.
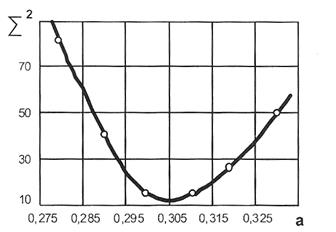
Рис.7.7
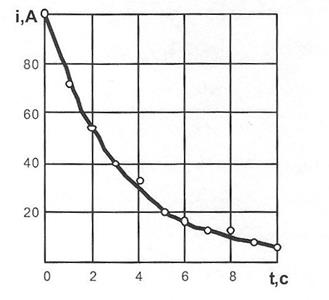
Рис.7.8
Завдання 8. Розглянемо результати експерименту щодо визначення статичної характеристики підсилювача:
| i, мА | ||||||||||||
| І, А |
Виразимо залежність І = f (i) лінійною залежністю: І=d0+d1i.
Тут І- сила струму завантаження; і- сила струму керування.
Для знаходження коефіцієнтів d0 і d1 скористаємося методом найменших квадратів:
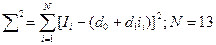
Візьмемо часткові похідні від 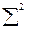 за змінними d0 і d1 і прирівнявши їх до нуля, одержимо:
за змінними d0 і d1 і прирівнявши їх до нуля, одержимо:
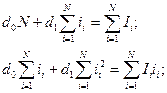
Вирішення системи дає значення спутаних коефіцієнтів.
Завдання 9. Для умов, указаних в попередньому завданні, перевірити адекватність одержаної залежності І=0,687+0,124і при дисперсії досліду Dt0=0.8 2A2 і числі паралельних вимірювань в кожній точці m=3.
За даними експерименту обчислюємо дисперсію адекватності:
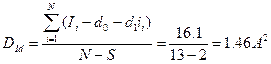
Оскільки 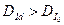 для оцінки адекватності знаходимо значення критерію Фішера:
для оцінки адекватності знаходимо значення критерію Фішера:
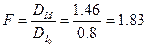
Значення Ім встановлене за таблицею критерію Фішера, при ступенях свободи 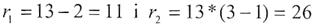
дорівнює 2,19. Таким чином F<Fm і знайдена залежність адекватно описує досліджуване явище.
У розглянутому випадку згідно з результатами експерименту
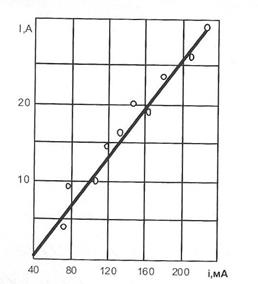
Рис.7.9
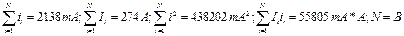
Підставивши ці значення, одержимо d0=0.687A і d1=0.124 A/мА.
Тоді залежність I = f (i) набуде вигляду І=0,687+0,124і.
Додаток 1
Значення t–критерію Стьюдента при 5%-му рівні значущості.
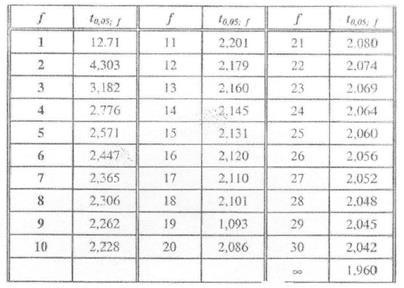
Додаток 2
Значення t–критерію Стьюдента при 1%-му рівні значущості
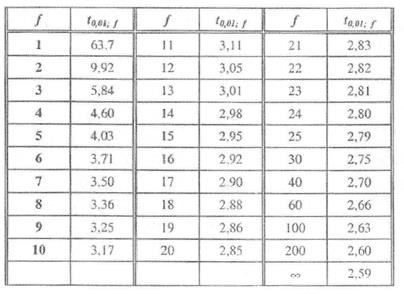
Додаток 3
Значення F–критерію Фішера при 5%-му рівні значущості
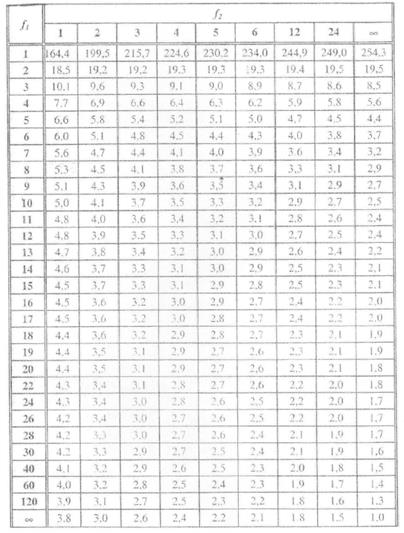
Додаток 4
Значення F–критерію Фішера при 1%-му рівні значущості
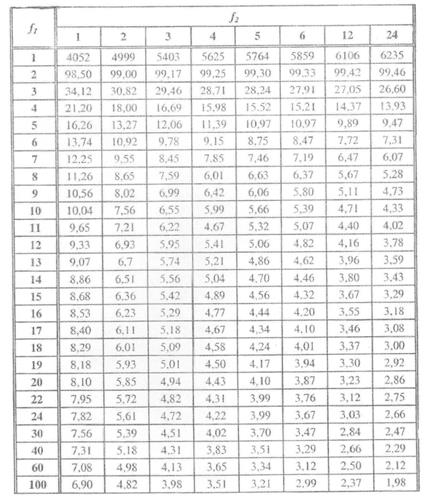
Додаток 5
Таблиця номінальних значень найпоширеніших факторі впливу та їх меж для нормальних умов застосування засобів вимірювальної техніки
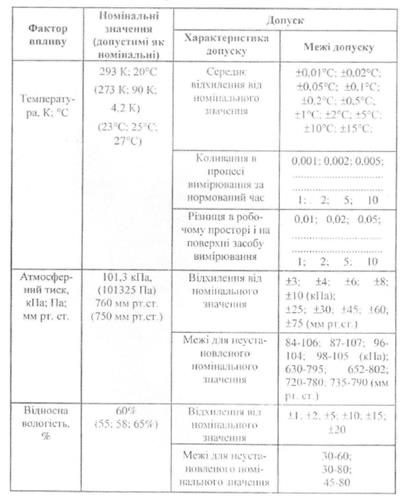
Продовження.дод.5
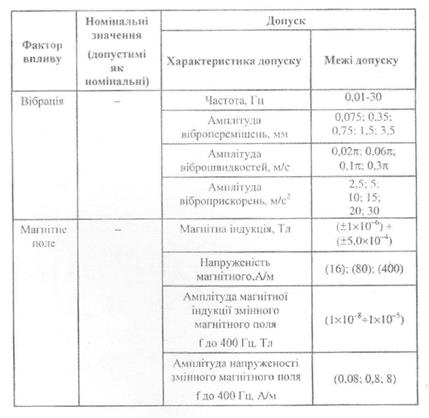
Додаток 6
Значення X2af для значеннь a i f
Date: 2015-09-19; view: 955; Нарушение авторских прав