
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Дрібний факторний експеримент
|
|
План і модель – нерозривно зв’язані поняття. Неможливо приступити до вибору плану без завдання моделі об’єкта. Наприклад, треба встановити, які плани необхідно використовувати, якщо мова іде про лінійну модель і взаємодію, що можна знехтувати.
Кількіс ть дослідів в ПФЕ 2 k при К≥3 значно перевищує число лінійних коефіцієнтів. Зокрема, при К=3 кількість дослідів N=8, а число коефіцієнтів дорівнює чотирьом, тобто ПФЕ типу 2³ дає надмірну інформацію, яка несуттєва при побудові лінійної моделі. Для зменшення кількості дослідів і збереженні властивостей, притаманних ПФЕ 2 k, користуються дрібним факторним експериментом (дрібною реплікою). Такий план являє собою частину плану ПФЕ. Наприклад, для випадку вивчення трьох факторів матриця планування ПФЕ 2³ має вигляд, показаний в табл. 4.8.
План ПФЕ 2² тут обведено рамкою.
При нехтуванні ефектом взаємодії вектор-стовпець x1 x2 плану ПФЕ 2² можна використовувати для введення в цей план нового фактора x3, що дозволяє визначити лінійну модель об’єкта у вигляді Y=b0+b1x1+ b2x2+ b3x3
Таблиця 4.8 - Матриця планування трикратного експерименту
| № досліду | x0 | x1 | x2 | x3 | x1 x2 | x1 x3 | x2 x3 | x1 x2 x3 | Y |
| +1 | -1 | -1 | -1 | +1 | +1 | +1 | -1 | Y1 | |
| +1 | +1 | -1 | -1 | -1 | -1 | +1 | +1 | Y2 | |
| +1 | -1 | +1 | -1 | -1 | +1 | -1 | +1 | Y3 | |
| +1 | +1 | +1 | -1 | +1 | -1 | -1 | -1 | Y4 | |
| +1 | -1 | -1 | +1 | +1 | -1 | -1 | +1 | Y5 | |
| +1 | +1 | -1 | +1 | -1 | +1 | -1 | -1 | Y6 | |
| +1 | -1 | +1 | +1 | -1 | -1 | +1 | -1 | Y7 | |
| +1 | +1 | +1 | +1 | +1 | +1 | +1 | +1 | Y8 |
У загальному випадку дрібна репліка відповідає плану ПФЕ типу 2 k-r де показник r, r = 1,2…, характеризує дрібність репліки відносно плану 2 k.
Відмітимо, що ефективність застосування дрібних реплік підвищується із зростанням числа факторів. Так при дослідженні впливу шести факторів на лінійні моделі можна в b разів скоротити число дослідів, використавши репліку більшої дрібності (при r = 3 дрібність репліки складає 1/8 від плану ПФЕ 2 6 і замість 64 дослідів проводяться 8).
4.8 Складання планів другого порядку
У тих випадках, коли поверхня відклику суттєво нелінійна в рівнянні моделі крім лінійних членів і членів, що враховують взаємодію, необхідно, як мінімум включати й квадратичні члени, які дозволяють відобразити не лінійність яких-небудь переріз ів поверхні відклику. Як і раніше, завданняпланування експерименту полягає у визначенні: за виміряними значеннямивідгуку Yі коефіцієнтів апроксимуючого полінома, що включає в себе квадратичні члени. Зокрема, при двофакторному експерименті така модель має вигляд
 (4.5)
(4.5)
Спроба оцінити коефіцієнти полінома за планом ПФЕ 2² не дає позитивних результатів. Дійсно, при побудові вектор-стовпців для x4=x12 I x5=x22 одержимо стовпчики, які співпадають один з одним і з стовпчиком x.Оскільки вказані с товпці не відмінні, неможливо визначити, за рахунок чого формується значення b 0; воно залежить як власне від b 0, так і від внесків квадратичних членів, тобто має місце змішана оцінка. Це твердження справедливе і при більшій кількос ті факторів. Причина полягає в тому, що для характеристики кривизни поверхні відгуку в перерізі Y=f(xi) при x= const, i 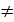 j необхідно не менше трьох точок, а дворівневі плани дозволяють встановити тільки дві точки. Таким чином, з планів ПФЕ типу 2² неможливо одержати інформацію про коефіцієнти b ii при квадратичних членах і членах більш високого порядку. Це завдання може бути вирішена при переході до плану ПФЕ з більшим числом рівнів варіювання факторів, наприклад до плану ПФЕ типу 3 k. Проте тоді число дослідів стає досить великим навіть при порівняно малому числі факторів (табл. 4.9)
j необхідно не менше трьох точок, а дворівневі плани дозволяють встановити тільки дві точки. Таким чином, з планів ПФЕ типу 2² неможливо одержати інформацію про коефіцієнти b ii при квадратичних членах і членах більш високого порядку. Це завдання може бути вирішена при переході до плану ПФЕ з більшим числом рівнів варіювання факторів, наприклад до плану ПФЕ типу 3 k. Проте тоді число дослідів стає досить великим навіть при порівняно малому числі факторів (табл. 4.9)
Більш простим шляхом рішення є добудова плану ПФЕ 2 k (або його дрібної репліки) до плану більш високого порядку. В цьому раз і план ПФЕ 2ⁿ приймають за ядро або центр плану другого порядку, а потім до нього додають симетрично розташовані допоміжні точки факторного простору, які називаються зірковими. Іншими словами, крім значень факторів на рівнях ±1 на кожній координатній осі факторного прос тору вибирають дві з іркові точки 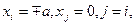 а також додають точку початку координат i x = 0, і=1,к. У кожній площині, що проходить через центр і утримує вісь Y і координатну вісь і-го фактора, маєють місце три значення фактора xi(-a;0;+a) і три відповідних значення Y. Загальне число дослідів у плані, побудованому таким чином при k>1, складає
а також додають точку початку координат i x = 0, і=1,к. У кожній площині, що проходить через центр і утримує вісь Y і координатну вісь і-го фактора, маєють місце три значення фактора xi(-a;0;+a) і три відповідних значення Y. Загальне число дослідів у плані, побудованому таким чином при k>1, складає
N = 2 k + 2 k + 1.
Відмітимо, що число дослідів, визначене цим співвідношенням, суттєво менше ніж, наприклад, у плані ПФЕ 3 k при k>2.
Таблиця 4.9
| Кількість факторів k | Кількість коефіцієнтів квадратичного полінома
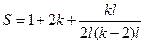
| Число дослідів при плані | ||
ПФЕ 2k,
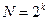
| ПФЕ 3k,
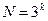
| Другого порядку,
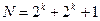
| ||
4.9 Ортогональні центрально-композиційні плани
Обробка даних експерименту пов’язана з вирішенням досить громіздкої системи нормальних рівнянь. Щоб запобігти цьому добудову ПФЕ 2 k (вибір положення з іркових точок) треба робити таким чином, щоб виконувались принципи ортогональності і симетрії. Умови нормування можуть не додержуватися. План другого порядку, задовольняючи і цим умовам, прийнято називати ортогональним центрально-композиційним планом (ОЦКП).
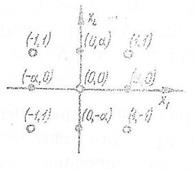
Рис. 4.3
Як приклад розглянемо розташування дослідних точок у двофакторному просторі ОЦКП. На рис. 4.3 кружками відмічені точки ядра плану (план ПФЕ2²), а точками - зіркові точки.
Величина a, яка називається зірковим плечем, залежить від числаварійованих факторів. Щоб матриця планування була ортогональною, алгебраїчна сума елементів вектор-стовпців повинна дорівнювати нулю не тільки для кожного фактора і їх добутку, але й для вектор-стовпців відповідних квадратам факторів. Очевидно, що виконати останню умову можливо лише в тому раз і, якщо квадрати факторів піддати деякому перетворенню, оскільки в противному раз і сума квадратів будь-яких чисел не дорівнює нулю. Найпрос тішим перетворенням квадратів факторів є наступні:
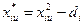 (4.6)
(4.6)
де 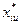 - перетворений фактор; d i – постійна величина, що залежить від числа факторів k. Запишемо умови симетрії для квадратів факторів з урахуванням співвідношення (4.6):
- перетворений фактор; d i – постійна величина, що залежить від числа факторів k. Запишемо умови симетрії для квадратів факторів з урахуванням співвідношення (4.6):
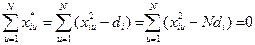 (4.7)
(4.7)
Звідси 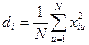
При 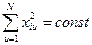 значення di однакове для всіх факторів.
значення di однакове для всіх факторів.
Для перетворених факторів повинна також виконуватись умова ортогональнос ті:
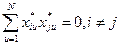 (4.8)
(4.8)
Вона задовольняється при значеннях зіркового плеча a, наведених у табл. 4.10. У цій таблиці є ще інші дані, необхідні для визначення коефіцієнтів квадратичних поліномів.
Таблиця 4.10 - Дані для розрахунку коефіцієнтів полінома
| Число факторів, k | Ядро плану ПФЕ | Загальне число дослідів, N | Зіркове число, α | Значення d |
| 22 | 1.000 | 0.667 | ||
| 23 | 1.215 | 0.730 | ||
| 24 | 1.414 | 0.800 | ||
| 25-1 | 1.547 | 0.770 | ||
| 25 | 1.596 | 0.863 |
Маючи дані таблиці, можна побудувати ОЦКП другого порядку. Приклад такого плану для двох факторів (a=1),(d=2/3) наведений в табл. 4.11.
Таблиця 4.11 - ОЦКП другого порядку для двофакторного експерименту
| Пара-метри | 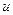
| 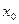
| 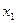
| 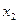
| 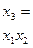
| 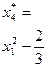
| 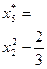
| 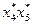
|
| План ПФЕ 22 | +1 | -1 | -1 | +1 | 1/3 | 1/3 | 1/9 | |
| +1 | +1 | -1 | -1 | 1/3 | 1/3 | 1/9 | ||
| +1 | -1 | +1 | -1 | 1/3 | 1/3 | 1/9 | ||
| +1 | +1 | +1 | +1 | 1/3 | 1/3 | 1/9 | ||
| Зіркові точки | +1 | -1 | 1/3 | -2/3 | -2/9 | |||
| +1 | +1 | 1/3 | -2/3 | -2/9 | ||||
| +1 | -1 | -2/3 | 1/3 | -2/9 | ||||
| +1 | -2/3 | 1/3 | -2/3 | |||||
| Нульо-ва точка | +1 | -2/3 | -2/3 | 4/9 |
Аналіз даних таблиці свідчить, що умови (4.7) і (4.8) виконуються. Це дозволяє визначити коефіцієнти апроксимуючого полінома. Поліном (4.5) зурахуванням перетворення (4.6) записується так:
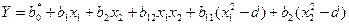
Після розкриття дужок поліном можна привести до звичайного вигляду:
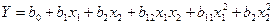 (4.9)
(4.9)
де 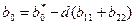
Проілюс труємо викладене на прос тому прикладі.
Приклад. Нехай в результаті дослідів за планом ПФЕ 2² (див. табл. 4.11 u= 1, 4) одержані значення функції відклику Y, наведені нижче:
Таблиця 4.12 - Значення функції відгуку
| Відгук | № досліду u | ||||||||
| У досліді Y, | 6.00 | 3.00 | 4.00 | 7.00 | 5.00 | 5.00 | 1.00 | 3.00 | 2.00 |
| Розра-хунок Yp | 5.83 | 2.83 | 4.17 | 7.17 | 5.00 | 5.00 | 1.33 | 2.67 | 2.00 |
Коефіцієнти bi апроксимуючого полінома, які враховують лінійні ефекти і ефекти взаємодії, розраховують за формулою
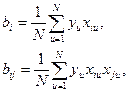
У даному випадку і = 0, 3, N – 4. Після підстановки в цей вираз значень
Y u і X iu остаточно одержимо: b0 = 5; b1 0; b2 = 0, 5; b12 =1,5.
Апроксимуючий поліном запишемо у вигляді
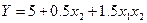
Оскільки в даному разі кількість дослідів N і кількість коефіцієнтів полінома співпадають (N = S = 4), апроксимуюча поверхня проходить через всі чотири дослідні точки. Для перевірки адекватнос ті залежності по всій поверхні експериментування поставимо контрольний дослід у нульовій точці x = x = 0, u = 9. Експериментальним значенням функції відгуку Y e 9 = 2, що суттєво відрізняється від розрахованого її значення Y p 9 = 5 ( Y = 3). Для одержання кращої апроксимації функції відгуку добудуємо план до ортогонального плану другого порядку, тобто до чотирьох дослідів, плану ПФЕ 2² і досліду в нульовій точці додамо чотири досліди (u = 5, 8) в зіркових точках.
Y = 3). Для одержання кращої апроксимації функції відгуку добудуємо план до ортогонального плану другого порядку, тобто до чотирьох дослідів, плану ПФЕ 2² і досліду в нульовій точці додамо чотири досліди (u = 5, 8) в зіркових точках.
Коефіцієнти квадратичного полінома (4.9) знаходять за формулою
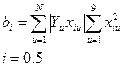
Остаточно маємо: 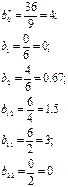
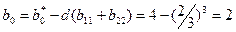
Підставимо знайдені значення коефіцієнтів в (4.9) і запишемо:
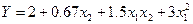 (4.10)
(4.10)
Розраховані значення функції відклику Y, обчислені відповідно до (4.10) наведені в табл. 4.12. Як видно з цієї таблиці, точність апроксимації суттєво підвищується:
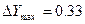
Date: 2015-09-19; view: 879; Нарушение авторских прав