Класичні методи визначення екстремуму

За класичними методами пошукові досліди для просування до облас ті екстремуму виконують шляхом почергового варіювання незалежних змінних. При цьому вважається, що всі інші фактори залишаються на цей час незмінними (фіксованими).

Зобразимо функцію відгуку досліджуваного об’єкта топографічним способом за допомогою замкнутих ліній постійного рівня (рис. 5.1), використовуючи метод Гаусса-Зейделя.

Вибираємо (або задаємо) базову точку K₀ (Х₀₁, Х0₂, …, Х_0n), де n – число керованих вхідних величин. Потім вибираємо с тупінь варіювання незалежними змінними. Він повинен бути не дуже малим, щоб рух до екстремуму не був повільним, а вибір кроку дуже великим що може призвести до грубих похибок у знаходженні екстремуму.

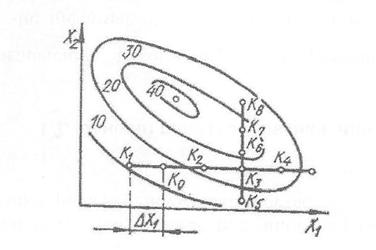
Рис. 5.1 - До використання методу Гауса-Зейделя

Відповідно до методу Гаусса-Зейделя, на першому етапі стабілізуємо усі незалежні змінні, крім першої, на рівні 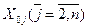, а змінну Х₁ варіюємо за обраним кроком.

Таким чином, в околиці базової точки К0 проводимо два досліди при значеннях Х₁₁=Х₀₁-ΔХ₁ і Х₂₁=Х₀₁+Х₁ і знаходимо відповідно значення функції відгуку Y₁і Y₂ в точках K₁ і K₂ (ΔХ₁ – крок варіювання незалежної змінної Х₁). Порівнюючи Y(X₁₁) і Y(X₂₁), встановлюємо напрямок зміни Х₁, який приводить до збільшення функції відгуку Y(X). Для випадку, представленого на рис. 5.1, значення функції відгуку в точці K₂ більше ніж у точці K₁. У такій ситуації рухатися необхідно в напрямку K₀ - K₂ за обраним кроком ΔХ₁. Процедура просування до локального (часткового) екстремуму за фактором Х₁ закінчується, коли для будь-яких трьох послідовних точок Х_(m-1),1, Х _m,1, Х_(m+1),1 виконується Y _m-1 < Y_m > Y _m+1. Точка K_m відповідає локальному екстремуму і вибирається базовою, значення Х_m фіксується і першій етап завершується. Для випадку, представленого на рис. 5.1 такою точкою є точка K₃.

На другому етапі точка першого час ткового екстремуму приймається за нову базову точку, і варіюється друга незалежна змінна Х₂ зі своїм ступенем варіювання ΔХ₂, а інші фактори стабілізуються. Знову виконуємо пробні досліди для виявлення напрямку руху до екстремуму за фактором Х ₂, а потім проводимо рухи для досягнення часткового екстремуму.

Для прикладу на рис. 5.1 рух до екстремуму після проведення пробних дослідів необхідно виконувати в напрямку K₃ – K₆ для досягнення точки K₇, яка приймається за нову базову точку. Якщо число незалежних змінних n, то на третьому етапі варіюється Х₃ при стабілізованих інших Х_j і т.д. до знаходження часткового екстремуму за n-м фактором. Якщо головний екстремум не досягнуто, то проводимо новий цикл дослідів з n етапів і т.д. до досягнення головного екстремуму.

Очевидною перевагою методу Гаусса-Зейделя є його наглядність і простота. Проте шлях до головного (глобального) екстремуму звичайно буває довгим, особливо при великому числі n змінних. Крім того, при цьому важко стабілізувати на довгий час всі керовані фактори, крім одного, що викликає допоміжні похибки в знаходженні часткових екстремумів.

Застосування градієнтних методів дозволяє швидше відшукати область екстремуму. Ці методи засновані на попередньому визначенні градієнта функції відгуку Y(Х) = Y(Х₁, Х₂, …, Х_n). Градієнтом непереривної функції Y(Х) називається вектор з координатами

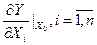
де Х₀ = (Х₀₁, Х₀₂, …, Х_0n) – точка, в якій береться градієнт:

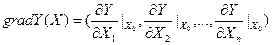(5.1)

Якщо функцію відгуку в околиці точки Х₀ розкласти в ряд Тейлора й обмежитись лише лінійними членами, то область, розташовану біля Х₀, можна апроксимувати залежністю

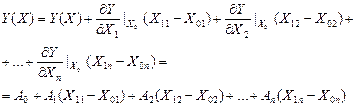(5.2)

Порівнюючи (5.1) і (5.2), неважко зробити висновок, що координати вектор-градієнта по відношенню до точок А0, співпадають з коефіцієнтами А₁,А₂, …, А_n лінійної поліноміальної моделі.

Методи градієнта відрізняються правилом вибору кроку просування до екстремуму. Суть стратегії всіх градієнтних методів полягає в тому, що на кожному етапі руху до екстремуму біля обраної (або одержаної) базової точки проводять пробні досліди, за результатами яких оцінюють напрямок градієнта у факторному прос торі, після чого виконують за обраним робочим кроком λ просування в нову базову точку, яка буде ближче до екстремуму ніж початкова 100 точка. Таким чином, градієнтним називають метод, відповідно до якого точка Х _m+1 вибирається з умови

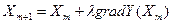(5.3)

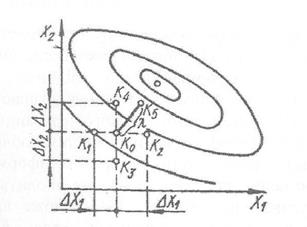
Рис. 5.2 - До використання градієнтного методу

На рис. 5.2 показано порядок проведення дослідів за методом градієнта.

Як і за методом Гаусса-Зейделя, в околиці базової точки ставимо досліди для відшукання напрямку просування (в даному разі в напрямку градієнта).

Вибираємо ступені варіювання ΔХ₁, ΔХ₂ незалежними змінними. Слід враховувати, що при малих с тупенях варіювання ΔХ_j (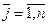) може бути велика похибка оцінки складових градієнта, а при дуже великих – можна не враховувати особливості рельєфу в околиці базової точки поверхні відгуку.

Пробні досліди в точках K₁, K₂, K₃, K₄ дають значення функції відгуку в цих точках. Складові градієнта за змінними Х₁ і Х₂ обчислюються на основі результатів пробних дослідів як відношення прирос ту функції відгуку Y _у відповідних точках до приросту аргументу в тих же точках:

Згідно з (5.2) було встановлено, що складові градієнта є оцінками коефіцієнтів Аj в даному випадку рівняння площини

яка апроксимує поверхню відгуку в районі базової точки K₀.

Напрямок градієнта K₀K₅ при обраному кроку λ будуємо так, щоб проекція K₀K₅ на вісь Х₁ була пропорційна 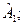, а на вісь Х₂ – пропорційна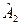

Для цього помножимо крок просування до екстремуму λ на відповідне значення коефіцієнта А_j і одержимо добутки 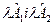які відповідають другій складовій у правій частині виразу (5.3).

Одержані значення відкладаємо у масштабі (перераховуємо) від базової точки K0 уздовж осей Х₁, Х₂ з урахуванням знака 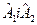. Якщо відшукується максимум функції відгуку, то при 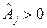цей добуток відкладається в позитивному напрямку осі Х_j, а при 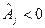– у від’ємному.

Таким чином, одержують координати нової базової точки K₅, в околиці якої вже описаним способом ставиться нова серія пробних дослідів, за результатами яких оцінюється новий напрямок градієнта. Кроки просування до екстремуму й пробні досліди продовжують до тих пір, поки всі значення А_j не стануть нехтуючи малими. Це й буде ознакою попадання чергової базової точки в область екстремуму.

Модифікації класичного градієнтного методу відрізняються правилом вибору кроку λ просування до екстремальної облас ті. Так, за методом Кіфера- Вольфовіца значення пробних приростів ΔХ_j і параметр кроку λ зменшуються в міру наближення до екстремальної облас ті (залежно від номера кроку).

Градієнтному методу в порівнянні з методом Гаусса-Зейделя, властива більша швидкіс ть просування до екстремуму. Проте він більш «чутливий» до випадкових вад – похибка у визначенні проекцій градієнта дуже впливає на правильність вибору напрямку кроку. Градієнтний метод при здійсненні пробних дослідів припускає також фіксацію регульованих змінних при варіюванні однією з них.

Date: 2015-09-19; view: 494; Нарушение авторских прав