Оцінка значущості коефіцієнтів апроксимуючої залежності, взятій у вигляді алгебраїчного полінома, в сенсі відмінності значень цих коефіцієнтів від нуля

Таку оцінку виконують окремо для кожного коефіцієнта i a за допомогою критерію Ст'юдента:

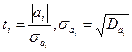
Де D a_j - дисперсія коефіцієнта регресії a_i.

Величину D a_j визначають наступним чином. Вирішують систему нормальних рівнянь відносно коефіцієнтів a_i, але при цьому праві частини

не заміняють їх числовими значеннями. У результаті вирішення для коефіцієнтів a_i знаходять лінійні залежності від величин v_i Якщо в ці залежності підставити числові величини v_i, то отримаємо числові коефіцієнти a_i. Якщо ж в них підс тавити замість v_i одиницю, а замість інших v_i нуль, то можна отримати для кожного a_i значення M_i, за допомогою якого ізнаходиться D a_j

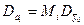
Зокрема, при лінійній залежності y=a₀+a₁x і умові 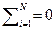(цього завжди можна досягти, якщо прийняти середньоарифметичну величину x за початок відрахунку) залежніс ть має вигляді

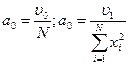
Тоді при v_i=1 маємо M₀=N^-1

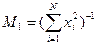
Можна тоді записати

Значення t_i, встановлене за формулою, порівнюємо з табличним t_Т знайденим для числа ступенів свободи v=N(m-1) для прийнятого рівня значущості.

Якщо 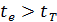, коефіцієнт a_e вважається незначним (тобто можна прийняти a_e=) і відповідна складова вираховується з рівняння регресії.

Відмітимо, що при m =1 маємо v=0 і розглянутий метод оцінки не можна застосовувати. У цьому випадку оцінка значущості коефіцієнта може бути виконана шляхом порівняння дисперсії адекватності D _ya при наявності члена апроксимуючого полінома з коефіцієнтом i a і за його відсутнос ті. Якщо дисперсія для другого варіанта близька до дисперсії для першого (або менше), то розглядуваний коефіцієнт можна вважати незначним.

Date: 2015-09-19; view: 445; Нарушение авторских прав