
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Однофакторний дисперсійний аналіз
|
|
Розглянемо ідеальний варіант – випадкові впливи відсутні, необхідно дослідити вплив тільки одного фактора. Найкращою оцінкою впливу фактора може служити величина, аналогічна дисперсії, що характеризує розсіяння вихідної величини і у ~ біля деякого середнього значення. Проте не треба забувати, що в даному разі спостерігається тільки аналогія з дисперсіями, оскільки 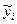 - детерміновані величини, такі величини, які впливають і похибки сприйняття відсутні.
- детерміновані величини, такі величини, які впливають і похибки сприйняття відсутні.
Тоді кількісна оцінка впливу фактора може бути подана у вигляді
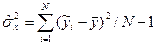
де N – кількіс ть приладів (рівнів), кожним з яких проводиться одне вимірювання.
У дійсності спостерігається вплив випадкових неврахованих величин, які в сукупності можна позначити ε. Вплив їх представимо у вигляді 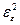 . При цьому дисперсія вихідної величини вже буде визначатися не тільки впливом фактора Х, але й випадковою величиною ε. Співставлення впливу цих величин через співставлення зумовлених ними дисперсій і є основою дисперсійного аналізу. Якщо досліджуваний фактор несуттєвий і дисперсія відтворюваності,яка характеризує один дослід, відома, то загальна дисперсія буде в основному визначатися дисперсією відтворюванос ті. Якщо ж фактор суттєвий, то можна вважати, що
. При цьому дисперсія вихідної величини вже буде визначатися не тільки впливом фактора Х, але й випадковою величиною ε. Співставлення впливу цих величин через співставлення зумовлених ними дисперсій і є основою дисперсійного аналізу. Якщо досліджуваний фактор несуттєвий і дисперсія відтворюваності,яка характеризує один дослід, відома, то загальна дисперсія буде в основному визначатися дисперсією відтворюванос ті. Якщо ж фактор суттєвий, то можна вважати, що
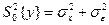
Виходячи з даного співвідношення, можна знайти дисперсію, яку зумовлює фактор, що вивчається. Звичайно дисперсія відтворюваності 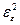 невідома, і її треба знайти за результатами експериментальних досліджень, тому проводять паралельні досліди для кожного рівня варіювання факторів.
невідома, і її треба знайти за результатами експериментальних досліджень, тому проводять паралельні досліди для кожного рівня варіювання факторів.
Вважатимемо, що дослідження об’єкта проводиться одночасно різними приладами з метою зменшення впливу фактора – приладу на результат дослідження (похибка показань). З’ясуємо, чи можна систематичні похибки приладів вважати однаковими.
Нехай число приладів буде N (фактор варіюється на N рівнях) і для кожного приладу (рівня) проводиться серія з m паралельних дослідів. Число дослідів при реалізації однофакторного дисперсійного аналізу буде N·m.
Результати дослідів наведені в табл. 6.1.
Таблиця 6.1
| i | l=1 | l=2 | … | l=m | 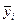
|

| 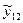
| … | 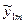
| 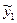
| |
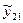
| 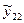
| … | 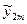
| 
| |
| . . . | … | … | … | … | … |
| N | 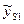
| 
| … | 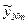
| 
|
За результатами дослідження для кожного і – го рівня незалежної змінної (різновиднос ті приладу) знаходять середнє значення (вважаємо однакову кратність проведення дослідів):
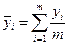
Розкид значень відгуків у фіксованому рядку (для конкретного приладу) визначається сукупною дією випадкових величин і характеризується оцінкою дисперсії відтворюванос ті. Розкид між середніми значеннями вихідних величин визначається впливом фактора. Якщо систематичні похибки приладів однакові, то треба чекати підвищеного розсіювання, вибіркових засобів середніх  .
.
Незміщена оцінка дисперсії відтворюванос ті для всієї сукупності дослідів визначиться у вигляді
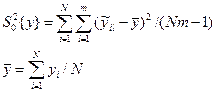
Розглянемо чисельник даного виразу 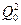 , вводячи під дужки
, вводячи під дужки 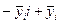
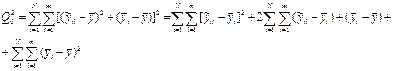
Розглянемо окремо другу складову в правій частині виразу 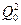

Оскільки сума відхилень від середнього в і – ій серії дорівнює нулю
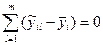
то і друга складова також дорівнює нулю.
Таким чином, повна сума квадратів відхилень окремих спостережень від 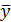 :
:
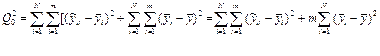
або в скороченому вигляді: 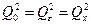
де 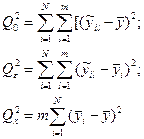
Складова  являє собою суму квадратів різниць між середніми окремих серій (рядків, прикладів) і загального середнього y за всією сукупністю спостережень і характеризує ступень розходження систематичних похибок в окремих прикладах. Її ще називають «розсіянням за факторами».
являє собою суму квадратів різниць між середніми окремих серій (рядків, прикладів) і загального середнього y за всією сукупністю спостережень і характеризує ступень розходження систематичних похибок в окремих прикладах. Її ще називають «розсіянням за факторами».
Складова 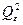 являє собою суму квадратів різниць між окремими спостереженнями і середнім відповідним серії
являє собою суму квадратів різниць між окремими спостереженнями і середнім відповідним серії 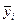 (середнє значення показів даного прикладу) і характеризує «залишкове розсіювання» випадкових похибок дослідів.
(середнє значення показів даного прикладу) і характеризує «залишкове розсіювання» випадкових похибок дослідів.
Таким чином, повне розсіювання показів приладів 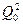 складається із двох компонент, характеризуючи розсіювання між приладами, тобто різниці між їх систематичними похибками
складається із двох компонент, характеризуючи розсіювання між приладами, тобто різниці між їх систематичними похибками  і розсіяння «в середині» приладів (серій), яке характеризує однакову (на основі передумов дисперсійного аналізу) для всіх приладів варіацію під дією випадкових величин
і розсіяння «в середині» приладів (серій), яке характеризує однакову (на основі передумов дисперсійного аналізу) для всіх приладів варіацію під дією випадкових величин 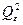 .
.
Вважаємо, що гіпотеза рівнос ті систематичних похибок правильна, тому нормальні розподіли для всіх приладів тотожні, тобто похибки мають однаковий центр розподілу (систематична похибка) і дисперсію 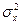 .У цьому випадку всі Nm спостережень можна розглядати як вибірку із однієї і тієї ж нормальної сукупності,a
.У цьому випадку всі Nm спостережень можна розглядати як вибірку із однієї і тієї ж нормальної сукупності,a 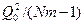 , як вже відмічалось, є незміщеною оцінкою дисперсії 2
, як вже відмічалось, є незміщеною оцінкою дисперсії 2 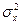 х за цією вибіркою.
х за цією вибіркою.
Звідси виходить, що відношення 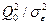 буде відповідати розподілу Х2 з (Nm-1) ступенями свободи.
буде відповідати розподілу Х2 з (Nm-1) ступенями свободи.
Проте середні за групами (приладами) 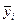 також згідно з припущенням нормально розподілені з дисперсією
також згідно з припущенням нормально розподілені з дисперсією 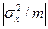 кожна, і незалежні одна від одної.
кожна, і незалежні одна від одної.
Тому
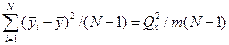
є незміщеною вибірковою характеристикою дисперсії 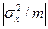 , одержаної на основі N спостережень величини
, одержаної на основі N спостережень величини 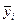 . У результаті можна зробити висновок, що величина
. У результаті можна зробити висновок, що величина
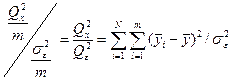
розподілена за законом Х2 з (N-1) ступенями свободи.
Сума квадратів відхилень від середнього в кожній серії, віднесена до дисперсії
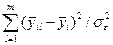
також розподілена за законом Х2 з (m-1) ступенями свободи.
Відповідні властивості композиції для N серій (приладів), компонента
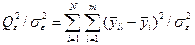
також розподілена за законом Х2 з N(m-1) ступенями свободи. Таким чином,
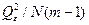 є також оцінкою параметра
є також оцінкою параметра 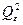
Із викладеного випливає, що у разі рівнос ті систематичних похибок приладів (несуттєвості впливу фактора, що досліджується) існують три незміщені оцінки 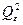 . Відношення двох однорідних оцінок дисперсій
. Відношення двох однорідних оцінок дисперсій
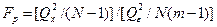 (6.1)
(6.1)
відповідатиме F - розподілу з (N-1) i N(m-1) ступенями свободи. Задаючись α рівнем значущості, на основі таблиці F- розподілу можна встановити відповідну α границю, так що

Розглянемо випадок, коли фактор, що досліджується, суттєвий, тобто гіпотеза про рівність систематичних похибок (центрів розподілу випадкових похибок) невірна, але параметр 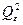 у всіх N сукупностях один і той же. Зміна центрів рядків розподілів, тобто зміна
у всіх N сукупностях один і той же. Зміна центрів рядків розподілів, тобто зміна 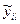 на
на  (де ci – систематична складова похибки і-го приладу) не змінить значення
(де ci – систематична складова похибки і-го приладу) не змінить значення 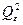 що, як і раніше, розподілено за законом Х2 з N(m-1) ступенями свободи, а
що, як і раніше, розподілено за законом Х2 з N(m-1) ступенями свободи, а 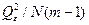 залишається незміщеною оцінкою
залишається незміщеною оцінкою 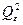 .
.
Проте чисельник виразу (6.1) саме враховує розходження між центрами розподілу ci і має тенденцію до збільшення при збільшенні розходження між систематичними складовими. Тому правило перевірки правильності висунутої гіпотези можна подати в наступному вигляді: гіпотеза c1=c2=…=Cn приймається, якщо 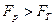 , і відкидається, якщо
, і відкидається, якщо 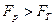 ,
,
Таблиця 6.2
| Компонента дисперсії | Середній квадрат | Ступінь свободи |
| Між факторами | 
| N-1 |
| Всередині серії | 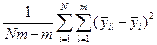
| N(m-1) |
| Повна (загальна) | 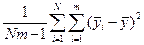
| Nm-1 |
Таблиця 6.3
| Номер прикладу | Результати вимірювання | ||||
| 98/-4 | 98/-2 | 79/-21 | 96/-4 | 96/-4 | |
| 107/+7 | 111/+11 | 130/+30 | 128/+28 | 127/+27 | |
| 119/+19 | 102/+2 | 87/-13 | 91/-9 | 102/+2 |
Схема однофакторного дисперсійного аналізу може бути предс тавлена у вигляді табл. 6.2, 6.3.
Розглянемо приклад застосування однофакторного дисперсійного аналізу для визначення відміннос ті систематичних похибок трьох приладів (N=3). Одне і те ж значення вихідної величини об’єкта дослідження вимірювалось цими приладами п’ять раз (кратніс ть проведення досліду – число дослідів всередині серії m=5). Одержані результати наведені в табл. 6.3. Для спрощення обчислень віднімемо з усіх граф таблиці число 100 (при цьому значення дисперсій не зміниться), а також використаємо такі співвідношення:

Таблиця 6.4
| i | 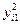
| 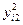
| 
| 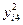
| 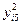
| 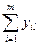
| 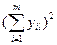
| 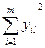
|
| -35 | ||||||||
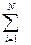
|
Перетворені значення результатів відтворювання наведені в знаменнику відповідної графи табл. 6.3. На основі ос таннього співвідношення одержимо зручні для розрахунку формули, що не потребують середніх значень. Для повної суми квадратів 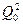 , беручи до уваги, що
, беручи до уваги, що 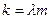
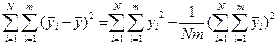
Для суми квадратів між приладами  ,
,
 (6.2)
(6.2)
Для суми квадратів всередині приладів 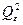
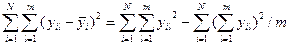 (6.3)
(6.3)
Для визначення  i
i 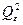 обчислимо відповідні складові вираз ів (6.2), (6.3), виходячи із табл. 6.3. Щоб оцінити, чи однакові систематичні похибки приладів N=3, необхідно, використовуючи вирази (6.2), (6.3) і дані табл. 6.4, знайти (при умові m=5):
обчислимо відповідні складові вираз ів (6.2), (6.3), виходячи із табл. 6.3. Щоб оцінити, чи однакові систематичні похибки приладів N=3, необхідно, використовуючи вирази (6.2), (6.3) і дані табл. 6.4, знайти (при умові m=5):
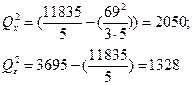
Число ступенів свободи визначаємо згідно з табл. 6.2:

Тепер можна перевірити нульову гіпотезу про рівність сис тематичних похибок приладів. Для цього знайдемо розраховані значення коефіцієнта
Фішера:
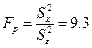
Порівняємо знайдене значення з табличним Fm. Задаючись рівнем статистичної значущості α=5%, за таблицею знайдемо значення Fm =3,88.
Таким чином  , тому гіпотеза про рівніс ть систематичних похибок приладів відкидається.
, тому гіпотеза про рівніс ть систематичних похибок приладів відкидається.
Якщо ж припущення про те, що дисперсія 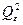 залишається однією і тією ж для всієї сукупності приладів, то можна знайти оцінку дисперсії
залишається однією і тією ж для всієї сукупності приладів, то можна знайти оцінку дисперсії  на основі того, що N(m-1)
на основі того, що N(m-1) 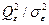 має розподіл Х2 з N(m-1) ступенями свободи і довірчий інтервал для неї. Дійсно, для і-го приладу при l -му вимірюванні
має розподіл Х2 з N(m-1) ступенями свободи і довірчий інтервал для неї. Дійсно, для і-го приладу при l -му вимірюванні
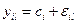
де ci – систематична похибка і – го приладу;
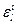 -та реалізація випадкової похибки. Тоді
-та реалізація випадкової похибки. Тоді
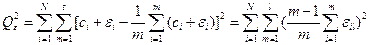
Звідки
 (6.4)
(6.4)
Як вже було сказано, для даного випадку
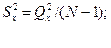
де 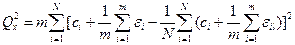
Позначимо 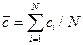 й одержимо
й одержимо
 (6.5)
(6.5)
Отже, дисперсія між приладами (факторами) несе інформацію як про дисперсію випадкової величини 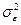 ,так і про усереднене відхилення систематичних похибок. Із виразів (6.4) і (6.5) випливає, що
,так і про усереднене відхилення систематичних похибок. Із виразів (6.4) і (6.5) випливає, що
 (6.6)
(6.6)
де 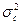 є мірою зміни систематичних похибок.
є мірою зміни систематичних похибок.
За результатами вибірки можна визначити оцінку 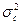 у вигляді
у вигляді
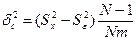
Крім того, за результатами проведеного дисперсійного аналізу можна оцінити розходження (неузгодженіс ть) між систематичними похибками і –го і j – го приладів. Для цього знайдемо значення коефіцієнта
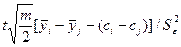
який відповідає розподілу Ст’юдента з N(m-1) ступенями свободи (в припущенні 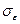 = const)
= const)
На основі знайденого коефіцієнта t за числом ступенів свободи N(m-1) можна визначити довірчий інтервал для різниці c i-c j у вигляді
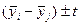
На практиці зустрічаються випадки, коли число спостережень в серіях різне. Позначивши через mі число спостережень і –ї групи (серії) при
 одержимо
одержимо
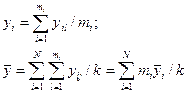
Основне співвідношення дисперсійного аналізу залишиться в нас тупному вигляді:
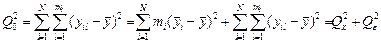
Розглянемо приклад проведення дисперсійного аналізу для випадку, коли число спостережень у групах різне. Для чотирьох складів гумової суміші перевіряли запас міцності на розтяг. Із кожного складу було виготовлено по чотири однакових зразка. Мета випробувань полягала у визначенні міцності кожного зразка, виборі найкращого і одержанні оцінки експериментальної похибки.
Таблиця 6.5
| A | B | C | D |
| 3210/42 | 3225/45 | 3220/44 | 3545/109 |
| 3000/0 | 3320/64 | 3410/82 | 3600/120 |
| 3315/63 | 3165/33 | 3320/64 | 3580/116 |
| - | 3145/29 | 3370/74 | 3185/97 |
Один із зразків суміші А за зовнішніми ознаками одразу був визнаний дефектним і виключений з випробувань. Результати досліджень наведені в чисельниках граф табл. 6.5.
Для спрощення обробки й аналізу даних віднімемо з кожного значення 3000 і поділимо на 5. Ці кодовані дані представлені в знаменниках граф. Прицьому відношення середніх квадратів не змінюється, а дисперсія випадкових величин складає 1/25 початкової. Після обчислень маємо:

Тоді середній квадрат між сумішами:
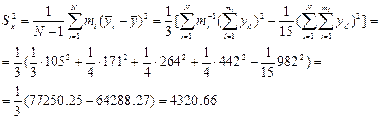
Середній квадрат всередині сумішей:
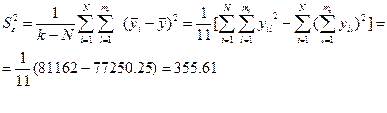
Розраховане значення коефіцієнта Фішера
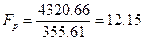
Табличне значення Fm за ступенями свободи з і 11 і (1-α) = 0,999 менше розрахованого, тому можна зробити висновок про різницю середнього запасу міцності на розтяг для чотирьох складів гумових сумішей.
95% довірчих інтервалів для середнього запасу міцності на розтяг кожної із цих сумішей визначаємо за формулою
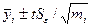
де t знаходимо з таблиці розподілу Ст’юдента за числом ступенів свободи 11, оскільки оцінка 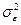 заснована на 11 ступенях свободи із загального числа їх
заснована на 11 ступенях свободи із загального числа їх
Date: 2015-09-19; view: 673; Нарушение авторских прав