
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Обробка результатів експерименту
|
|
Основною метою регресійного аналізу є одержання за результатами активного експерименту моделі, що адекватно описує поведінку досліджуваного об’єкту. Проведення експерименту повинно строго відповідати обраному випадковому порядку.
Коли є сумнів, що умови проведення дослідів залишаються постійними, то досліди в кожній точці факторного прос тору дублюються(проводиться серія дослідів).
Припустимо, що в кожній точці факторного прос тору, якій відповідає один з рядків матриці планування проводять серії із m дослідів. Для будь-якої і-точки обчислюють середнє значення вихідної величини:
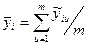
і рядкову дисперсію вихідної величини (точніше її оцінку):
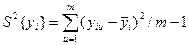
Знайдені таким чином рядкові дисперсії викорис товують для перевірки відтворюваності дослідів, яка полягає в перевірці одноріднос ті рядкових дисперсій – однієї з основних передумов множинного регресійного аналізу.
У подальшому будемо розглядати етапи обробки результатів експерименту на прикладі 2х факторного експерименту (табл. 4.5).
Таблиця 4.5
| № п/п | X0 | X1 | X2 | X1 X2 | y1i | y2i | y3i | yi | S2{yi} |
| +1 | -1 | -1 | +1 | ||||||
| +1 | +1 | -1 | -1 | ||||||
| +1 | -1 | +1 | -1 | ||||||
| +1 | +1 | +1 | +1 |
Знайдемо середні значення вихідної величини 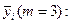
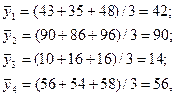
а також рядкову дисперсію вихідної величини:
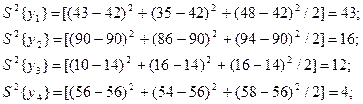
Серед, усієї сукупності розрахованих рядкових дисперсій визначаємо максимальне 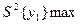 і беремо відношення даної дисперсії з суми всіх рядкових дисперсій
і беремо відношення даної дисперсії з суми всіх рядкових дисперсій 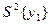 , тобто знаходимо коефіцієнт Кохрена:
, тобто знаходимо коефіцієнт Кохрена:
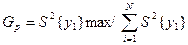
У разі ідеальної одноріднос ті коефіцієнт Gp прагне до значення 1/N. Розрахункове значення коефіцієнта Кохрена порівнюємо з табличним (критичного G-критерію), яке вибираємо із таблиці для прийнятого рівня значущості α і для чисел ступеня свободи f1=m-1, f2=N. Знаходимо розрахункове значення Gp=43/(43+16+12+4)=0,57.
Згідно з таблицею для α=0,05, f1=2, f2=4. Знаходимо GT=0.77; GT> Gp, тобто умова виконується. Пересвідчившись в однорідності, перейдемо до визначення оцінок коефіцієнтів за формулою
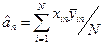
де n-номер вектор-стовпчика. Одержимо
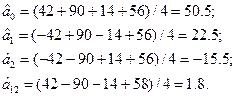
Знайдені таким чином коефіцієнти рівняння регресії необхідно оцінити на статистичну значущість. Оцінка виконуємо за t- критерієм Ст’юдента. Для кожного коефіцієнта 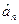 обчислюємо коефіцієнт
обчислюємо коефіцієнт 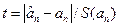 , тобто перевіряємо відхилення від нуля знайденої оцінки an .
, тобто перевіряємо відхилення від нуля знайденої оцінки an .
Тут 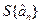 - оцінка середнього відхилення похибки визначення коефіцієнта.
- оцінка середнього відхилення похибки визначення коефіцієнта.
Оцінка дисперсії коефіцієнтів, знайдених за експериментальними даними:
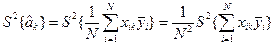
Беремо до уваги, що хіn у всіх дослідах в кодованому вигляді приймає значення +1 або – 1, тому для випадку незалежних випадкових величин хіn 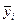 знак під знаком суми не впливає на результат. Крім того відомо, що дисперсіїсереднього
знак під знаком суми не впливає на результат. Крім того відомо, що дисперсіїсереднього 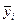 в m - разів менше дисперсії одного вимірювання(m- кратність проведення дослідів), тобто
в m - разів менше дисперсії одного вимірювання(m- кратність проведення дослідів), тобто
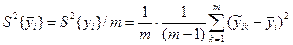
На основі вищесказаного і з урахуванням однорідності рядкових дисперсій можна записати
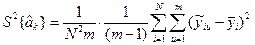
Оцінка генеральної дисперсії відтворюваності 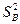 , що характеризує точність (усереднення) одного вимірювання, є середнє з усіх рядкових дисперсій:
, що характеризує точність (усереднення) одного вимірювання, є середнє з усіх рядкових дисперсій:
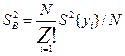
або
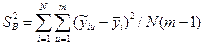
Таким чином, оцінку дисперсії коефіцієнта 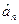 можна записати у вигляді
можна записати у вигляді
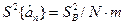
У деяких випадках, коли є впевненість, що дисперсії однорідні, оцінкою дисперсії відтворюваності може служить одна з рядкових дисперсій або оцінка дисперсії для будь-якої точки факторного простору (точніш за все це буває центр плану).
Коли число паралельних дослідів у кожній точці факторного прос тору різне, при усередненні однорідних дисперсій для оцінки дисперсіївідтворюваності корис туються середньозваженим значенням дисперсій, узятих з урахуванням ступенів свободи
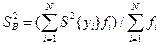
де- fi=mi-1- число ступенів свободи в і-му досліді, m - число паралельних дослідів.
Суть t- критерію Ст’юдента перевірки статистичної значущості знайдених оцінок коефіцієнтів полягає в наступному. Зміна вихідної величини залежить від впливу кожного члена апроксимуючого поліному і некерованих та неконтрольованих факторів.
Вплив n-го фактора, відхилення оцінки n-го коефіцієнта від нуля враховується коефіцієнтом 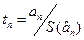 , вплив же некерованих і неконтрольованих факторів, а також похибки вимірювання вихідної величини можуть бути враховані за допомогою дисперсії відтворюваності 2 в S, яка має N(m-1) ступенів свободи (N-ступенів загублено при обчисленні рядкових середніх). При вибраному рівні статистичної значущості:α за таблицями розподілу Ст’юдента при числі ступенів свободи f= N (m-1)знаходять табличне значення коефіцієнта tтабл. Знайдене табличне значення порівнюють з розрахованим табличним значенням коефіцієнта. Якщо виконується нерівність tтабл.> tn, то приймається нуль-гіпотеза, тобто при обраному рівні статистичної значущості α (статис тичної достовірності 1-α) і числі ступенів свободи f вважається, що знайдений коефіцієнт
, вплив же некерованих і неконтрольованих факторів, а також похибки вимірювання вихідної величини можуть бути враховані за допомогою дисперсії відтворюваності 2 в S, яка має N(m-1) ступенів свободи (N-ступенів загублено при обчисленні рядкових середніх). При вибраному рівні статистичної значущості:α за таблицями розподілу Ст’юдента при числі ступенів свободи f= N (m-1)знаходять табличне значення коефіцієнта tтабл. Знайдене табличне значення порівнюють з розрахованим табличним значенням коефіцієнта. Якщо виконується нерівність tтабл.> tn, то приймається нуль-гіпотеза, тобто при обраному рівні статистичної значущості α (статис тичної достовірності 1-α) і числі ступенів свободи f вважається, що знайдений коефіцієнт 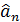 є статис тично незначним і його необхідно виключити із рівняння регресії.
є статис тично незначним і його необхідно виключити із рівняння регресії.
Таким чином, при виконанні умови (tтабл.> tn) неможливо визначити (в 100- α випадках), чим викликано зміна вихідної величини: впливом кожного члена рівняння регресії або впливом неврахованих факторів і наявніс тювипадкової похибки вимірювання вихідної величини.
Для розглянутого прикладу оцінка дисперс ії відтворюваності як оцінкаусереднених рядкових дисперсій згідно з таблицею буде

Як вже відмічалось, через властивіс ть нормування оцінки коефіцієнтів будуть знайдені з однаковою дисперсією, тобто
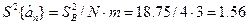
Тоді 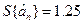
Знайдемо обчислене значення коефіцієнта Ст’юдента tn для встановлених оцінок коефіцієнтів 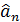
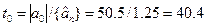
Аналогічно одержимо
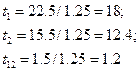
Із таблиці при рівні статистичної значущості α=5% і числі с тупенів свободи f= N (m-1)=4(3-1)=8 знайдемо табличне значення коефіцієнта. Воно дорівнює tт=2,3. Зіставимо розрахункове значення tn з табличним tтабл
Нерівніс ть виконується для t12. Таким чином, можна вважати, що коефіцієнт 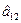 статистично незначний і його можна виключити з рівняння регресії – в данному випадку вплив парної взаємодії відсутній, але незначний проте перед тим якприйняти гіпотезу
статистично незначний і його можна виключити з рівняння регресії – в данному випадку вплив парної взаємодії відсутній, але незначний проте перед тим якприйняти гіпотезу  , необхідно переконатися у правильності пос тавленого експерименту. Може трапитися, що вибір діапазону вимірювання незалежної змінної (Х n max- Х n min) малий, а сумарна випадкова перешкода, накладена на вихідну величину об’єкта, значна. Це також може призвести до статистичної незначущості коефіцієнта. Пересвідчившись, що з цієї точки зору експеримент проведений правильно, можна
, необхідно переконатися у правильності пос тавленого експерименту. Може трапитися, що вибір діапазону вимірювання незалежної змінної (Х n max- Х n min) малий, а сумарна випадкова перешкода, накладена на вихідну величину об’єкта, значна. Це також може призвести до статистичної незначущості коефіцієнта. Пересвідчившись, що з цієї точки зору експеримент проведений правильно, можна 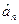 коефіцієнт виключити з рівняння регресії.
коефіцієнт виключити з рівняння регресії.
Оскільки повний факторний експеримент має властивості ортогональності, то виключення цього коефіцієнта з рівняння регресії не впливає на знайдені оцінки інших коефіцієнтів.
Таким чином, рівняння регресії досліджуваного об’єкта, який міс тить статистичні значущі коефіцієнти, буде (в кодованій системі)
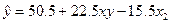
Для кожного коефіцієнта 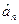 можна знайти довірчий інтеграл, в якому повинен попас ти істинний генеральний коефіцієнт з прийнятим рівнем значущості. Для цього використовуємо формулу
можна знайти довірчий інтеграл, в якому повинен попас ти істинний генеральний коефіцієнт з прийнятим рівнем значущості. Для цього використовуємо формулу
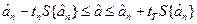
Отже, істинні значення коефіцієнтів моделі будуть знаходиться в межах
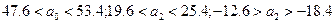
Одержане рівняння регресії, треба перевірити на адекватність досліджуваному об’єкту, тобто встановити, наскільки добре воно апроксимує одержані експериментальні дані. Для цього необхідно оцінити, наскільки відрізняються середні значення 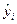 вихідної величини, одержаної в планах факторного простору в результаті проведення дослідів, і значення
вихідної величини, одержаної в планах факторного простору в результаті проведення дослідів, і значення 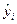 , одержаного з рівняння регресії в тих же точках факторного простору.
, одержаного з рівняння регресії в тих же точках факторного простору.
Для цього обчислюємо залишкову дисперсію, яку ще називають дисперсією адекватнос ті:
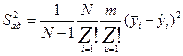
де m- число паралельних дослідів в і-й точці факторного простору, l-число здайдених в результаті проведених N - дослідів значущих коефіцієнтів.Якщо число паралельних дослідів різне, тоді оцінку дисперсії адекватності знаходимо із виразу
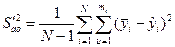
Відмінність S′ад2 від нуля пояснюється в загальному випадку двома причинами: дійсно неадекватністю рівняння регресії фізичному об’єкту (неправильно вибраний апроксимуючий поліном) і наявніс тю випадкової похибки сприйняття, що характеризується Sв2.
Якщо модель адекватна, то оцінки дисперсії відтворюванос ті залежать тільки від похибки сприйняття вихідної величини, зумовленої сумарною перешкодою, і в граничному випадку будуть однакові. Тому адекватність одержаної моделі перевіряємо шляхом порівняння оцінок двох дисперсій S′ад2 і Sв2 і F- критерію Фішера:
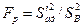
Знайдене Fр порівнюємо з табличним значенням Fт, яке встановлюємо при рівні статистичної значущості α і числі ступенів свободи fад=N-l I fв= N (m -1)
Якщо Fр< Fm, то одержана математична модель з прийнятим рівнем статистичної значущості α адекватна експериментальним даним і її можна використати для подальших досліджень. Повернемось до прикладу. Визначимо для одержаної моделі оцінку дисперсії адекватності.
Обчислимо значення 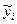 , які відповідають рядкам матриці плану:
, які відповідають рядкам матриці плану:
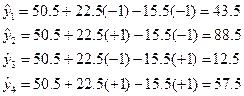
Оцінка дисперсії:
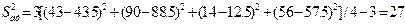
Одержане значення Sад2=27 розділимо на Sв2 =18,75 і одержимо F=1,44.
Табличне значення коефіцієнта Фішера на рівні статис тичної значущості α=0,05 і числі ступенів свободи fад=(4-3)=1 і fв= N (m -1)=4(3-1)=8 буде Fm=5,32.
Таким чином, при вибраному рівні статистичної значущості α=0,05 одержане в результаті експерименту 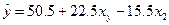 адекватнее досліджуваному об’єкту. Відмітимо, що дана модель представлена в кодованій системі координат. Щоб одержати її у звичайній системі, треба використати формули переходу.
адекватнее досліджуваному об’єкту. Відмітимо, що дана модель представлена в кодованій системі координат. Щоб одержати її у звичайній системі, треба використати формули переходу.
На практиці часто буває, що лінійне рівняння регресії незадовільно характеризує досліджувану область.
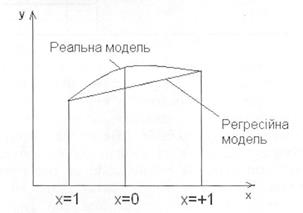
Рис.4.2 Перевірка адекватності лінійної моделі
На рис. 4.2 показаний випадок парної залежності, коли дослідні й розрахункові дані в точках, в яких проводився експеримент (у кодованій системі Х11= -1 і Х21=1) співпадають, проте всередині поля кореляції спостерігаються значні відхилення регресійної і реальних залежностей.
Для підвищення надійності перевірки адекватнос ті моделі час то проводять допоміжну серію паралельних дослідів у базовій точці xj=0, 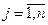 Тоді число точок факторного простору, за яким оцінюється адекватніс тьрівняння регресії, збільшують на одну і воно дорівнює N+1, тобто збільшується на одиницю і число ступенів свободи fад, що підвищує статис тичну надійніс тьприйнятих рішень. Однак базова точка не враховується в розрахункахкоефіцієнтів рівняння регресії. Значення вихідної величини в центрі плануповинно бути порівняне (в межах дисперсії відтворюваності) з вільним членомрівняння регресії, тобто
Тоді число точок факторного простору, за яким оцінюється адекватніс тьрівняння регресії, збільшують на одну і воно дорівнює N+1, тобто збільшується на одиницю і число ступенів свободи fад, що підвищує статис тичну надійніс тьприйнятих рішень. Однак базова точка не враховується в розрахункахкоефіцієнтів рівняння регресії. Значення вихідної величини в центрі плануповинно бути порівняне (в межах дисперсії відтворюваності) з вільним членомрівняння регресії, тобто
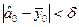
де - δ наперед задане значення, що залежить від Sв2.
У разі порушення цієї нерівності для математичного опису необхідні рівняння більш високого порядку.
Таблиця 4.6
| № п/п | x1 | x2 | x3 | 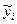
| x0 | x1 x2 | x1 x3 | x2 x3 | x1 x2 x3 |
| -1 | -1 | -1 | +1 | +1 | +1 | +1 | -1 | ||
| +1 | -1 | -1 | +1 | -1 | -1 | +1 | +1 | ||
| -1 | +1 | -1 | +1 | -1 | +1 | -1 | +1 | ||
| +1 | +1 | -1 | +1 | +1 | -1 | -1 | -1 | ||
| -1 | -1 | +1 | +1 | +1 | -1 | -1 | +1 | ||
| +1 | -1 | +1 | +1 | -1 | +1 | -1 | -1 | ||
| -1 | +1 | +1 | +1 | -1 | -1 | +1 | -1 | ||
| +1 | +1 | +1 | +1 | +1 | +1 | +1 | +1 |
Розглянемо ще один приклад побудови математичної моделі за результатами експерименту. Вважаємо, що на об’єкт діють три фактори:
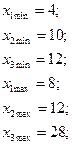
які пов’язані з вихідною величиною залежністю
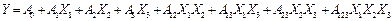
Середнє значення Xjcp=(X j max+X j min)і інтервал варіюваннянезалежних змінних 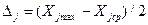 будуть
будуть
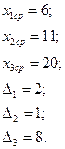
Підставимо значення X jcp і Аj у формулу переходу і одержимо рівняння моделі в кодованій системі координат:
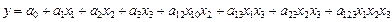
Оцінку коефіцієнтів цієї моделі будемо знаходити за експериментальними даними, одержаними в результаті проведення типу 2n, де n=3. Згідно з відомим правилом побудуємо матрицю повного трифакторного експерименту, яка має властивості ортогональнос ті симетричності і нормування (табл. 4.6).
Вважаємо, що досліди однорідні. Тому в кожній точці факторного простору можна проводити тільки за одним дослідом (серія паралельних дослідів не проводиться). Значення вихідної величини 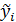 для цього випадку наведені у табл. 4.6.
для цього випадку наведені у табл. 4.6.
Для визначення оцінок коефіцієнтів рівняння регресії доповнимо матрицю плану (обведена більш жирними лініями) вектор-стовпцями фіктивної змінної і лінійними взаємодіями факторів.
За результатами експерименту визначимо оцінки коефіцієнтів:
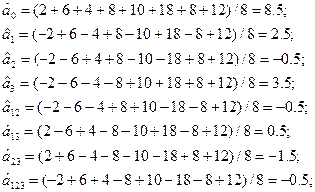
Для визначення оцінки дисперсії відтворюваності, а також більш достовірної перевірки адекватності одержаної моделі в центрі плану була поставлена допоміжна серія із р=3 дослідів і одержані наступні значення:
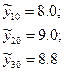
Середнє значення вихідної величини в центрі плану (х=0)
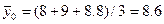
а дисперсія в центрі плану, яка приймається за оцінку дисперсії відтворюваності, визначається так:
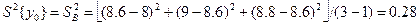
Оскільки виконується умова нормування, оцінки коефіцієнтів даної моделі будуть знайдені з однаковою дисперсією, тобто
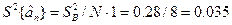
кратність досліду в кожній і-й точці (і=1, N) дорівнює одиниці, тобто m=1.
Звідки 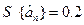
Перевіримо статистичну значущіс ть знайдених коефіцієнтів, встановимо розраховані значення коефіцієнта
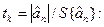
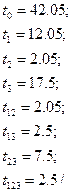
Табличне значення коефіцієнта Ст’юдента при α=0,05 і числі ступенів свободи (р-1)=(3-1)=2 (оцінка дисперсії відтворюваності проводилась на основі серії із р=3 дослідів в одній точці – центрі плану). 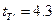
Порівнюючи табличне 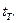 і обчислене tn значення коефіцієнтів, встановимо, що незначущими (так як
і обчислене tn значення коефіцієнтів, встановимо, що незначущими (так як 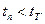 ) є знайдені оцінки коефіцієнтів
) є знайдені оцінки коефіцієнтів
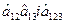
Рівняння регресії, яке має статистичні коефіцієнти,
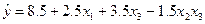
Одержану таким чином математичну модель необхідно перевірити на адекватність. Для цього визначимо оцінку дисперсії адекватності. Оскільки кратність дослідів дорівнює одиниці, тобто m=1, то
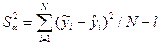
Попередньо переконавшись, що рівняння регресії “підходить” для опису експериментальних даних, оскільки середнє значення вихідної величини в центрі плану 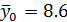 , а оцінка свобідного члена
, а оцінка свобідного члена  I
I 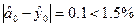 знайдемо значення вихідної величини на основі рівняння регресії в точках плану. Для першoї точки
знайдемо значення вихідної величини на основі рівняння регресії в точках плану. Для першoї точки
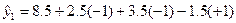
Аналогічно одержимо значення і для інших точок плану, які зведені в табл.3, виходячи з якої знайдемо оцінку дисперсії адекватності при умові, що N - l =8 -4(l =4), тобто уточнене рівняння регресії має чотири коефіцієнти:
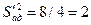
Знаючи значення S’2 aд встановимо обчислене значення коефіцієнта Фішера:
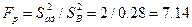
Таблиця 4.7
| № п/п | 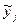
| 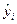
| 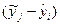
| 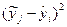
|

|
Число ступенів свободи f aд =(N-l)=4, fв=p-1=2. Задаючись рівнем статистичної значущості a=0,05, при f aд =4 і fв =2 в, знайдемо табличне значення FT=19.3.
Таким чином з достовірніс тю (1-α)=95% рівняння регресії адекватне експериментальним даним.
Одержане рівняння регресії предс тавлено в кодованій системі координат. Для переходу в звичайну систему координат скористуємося формулою переходу і значеннями хjср і Pj. Тоді
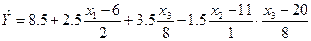
або
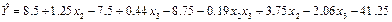
Остаточно одержимо рівняння регресії
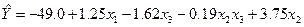 ,
,
що адекватно описує експериментальні дані.
Date: 2015-09-19; view: 714; Нарушение авторских прав