Факторні методи визначення екстремуму

До факторних методів пошуку екстремальної області відноситься метод крутого сходження (метод Бокса-Уілсона). Серед методів, що розглянуті теорією планування експерименту, метод крутого сходження (будемо розглядати знаходження максимуму функції відгуку) є з’єднуючим між початковим і кінцевим етапами дослідження. Головна ідея методу полягає в тому, що на початковому етапі на основі ПФЕ або ДФE одержують самі прості лінійні моделі в якості наближеного опису деякої час тини функції відгуку, далекої від екстремуму.

Коефіцієнти моделі, одержаної в результаті ПФЕ й ДФE, пропорційні проекціям вектор-градієнта й дозволяють оцінити саме напрямок градієнта, тобто напрямок самого крутого схилу поверхні відгуку. Потім уздовж цього напрямку відбувається поступовий кроковий рух до області екстремуму (звідси й сама назва методу). Метод крутого сходження (МКС) поєднує кращі властивості класичних методів – градієнтного й Гаусса-Зейделя. Схожіс ть із градієнтним методом полягає в тому, що при реалізації ІКС відбувається також просування до області екстремуму в напрямку градієнта, знайденого на основі пробних дослідів в околиці базової точки. Але на цьому схожість і закінчується. За класичним градієнтним методом проводять по два пробних досліди по обидві сторони від базової точки (рис. 5.2) шляхом почергового варіювання кожної із вхідних величин при стабілізації інших (n-1) факторів, а за МКС пробні досліди проводять відповідно до матриці плану ПФЕ або ДФE. За факторним експериментом в оцінці кожного коефіцієнту моделі, а значить, кожної складової градієнта беруть участь усі N точок (дослідів). Тому ці оцінки є більш точними, ніж при класичному градієнтному методі, де кожна складова градієнта обчислюється тільки за двома точками. Знайдений таким чином за МКС напрямок градієнта більш вадозахищений і дос товірний. У зв’язку з цим в знайденому напрямку градієнта можна виконати декілька, а не один, пробних кроків до досягнення часткового екстремуму. В цьому полягає схожіс ть МКС з методом Гаусса-Зейделя. Проте за класичним методом вважається фіксація (n1031) незалежної змінної при просуванні до екстремуму за варійованою змінною. Просування виконується уздовж осі - фактора, що сповільнює просування до області екстремуму. Таким чином, МКС дозволяє значно швидше й надійніше в порівнянні з класичними методами досягти екстремальної області. Крім того, МКС дає змогу одержати інформацію про ступінь крутизни поверхні в районі базової точки – ця інформація закладена в коефіцієнтах взаємодії.

Нехай задана базова точка K₀ (рис. 5.3). Приймемо її за центр плану, поставимо її в околиці ПФЕ (або ДФE). Важливою особливістю МКС є проведення с татистичної оцінки результатів ПФЕ, що значно підвищує надійність інтерпретації цих результатів.

Припустимо, що за результатами дослідів в області базової точки одержане лінійне рівняння регресії (в кодованій системі координат)

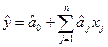
яке має статис тично значущі коефіцієнти. Вище було показано, що знайдені

оцінки коефіцієнтів 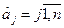пропорційні проекціям вектор-градієнта на осі -фактори.

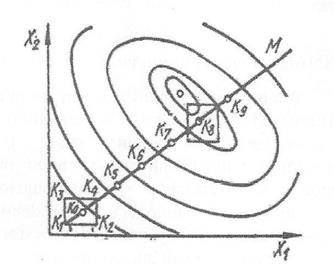
Рис. 5.3 - До використання методу крутого сходження (спуску)

Таким чином, за оцінками лінійних коефіцієнтів 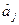можна оцінити й напрямок вектор-градієнта, за яким за обраним кроком можна здійснювати просування до час ткового екстремуму. Про досягнення часткового екстремуму, як за методом Гаусса-Зейделя, можна судити за нерівністю Y _m-1 < Y _m > Y _m+1. Якщо ця нерівність виконується, точка K_i є точкою час ткового екстремуму, її приймають за базову і в околиці реалізують ПФЕ або ДФE. Для випадку, наведеного на рис. 5.3, при просуванні в напрямку градієнта (промінь K₀M) такою точкою буде точка K₈.

У реальних умовах на досліджуваному об’єкті розглядають вхідні змінні в реальному масштабі, варіювання незалежних змінних у звичайних координатах. Повний або дрібний факторний експерименти дають значення функції відгуку в кодованій системі координат. Тому при оцінці складових градієнта треба враховувати значення ступенів варіювання за кожним фактором, а також те, що значення складових градієнта залежить і від масштабу вимірювання (представлення) факторів. Тому протягом всього експерименту незалежні змінні необхідно вимірювати (задавати) в одних і тих же одиницях, зберігати пос тійний масштаб.

Для обчислення координати точки Ki в напрямку градієнта при пошуку часткового екстремуму необхідно визначити взаємозв’язок між кроком варіювання j-ї незалежної змінної у звичайній і кодованій системі координат.

При цьому на основі рівняння регресії, одержаного за результатами ПФЕ або ДФE в околиці базової точки, встановлюють найбільш суттєвий фактор,наприклад k-й оцінка коефіцієнта за цим фактором за абсолютною величиною максимальна в порівнянні з іншими оцінками коефіцієнтів. Із фізичних міркувань, для даного фактора вибирають крок варіювання у природному масштабі λ_к виходячи з відомого співвідношення між значеннями фактора в кодованій хк і природній Хк системах координат:

(5.4)

де 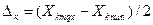, можна встановити взаємозв’зок між λ_к і нормованим кроком λ варіювання незалежної змінної в кодованій системі координат.

Оскільки точка зі значенням Х_ксер для пробного ПФЕ і ДФE лежить в центрі плану (див. рис. 5.3 точка К₀) і з неї починається просування доекстремуму в напрямку градієнта, то координата по Х_к першої точки в напрямку екстремуму (для розглянутого прикладу точки К₅) визначається як різниця

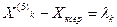(5.5)

На основі співвідношення (5.4) в кодованій системі координат одержимодля точки К₅

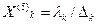(5.6)

Проте для кодованого значення к-го фактора для точки К₅ можназаписати

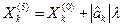
Як вже відмічалося, точка К₀ лежить в центрі плану, тому 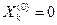i

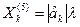(5.7)

Співставивши вирази (5.6) і (5.7) одержимо взаємозв’язок між кроком варіювання к-го фактора λ_к в натуральних одиницях з нормованим кроком варіювання λ в кодованих одиницях:

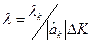(5.8)

Оскільки спочатку був вибраний крок варіювання найбільш суттєвої змінної λ_к, то для того, щоб просуватися в напрямку градієнта, знайденого на основі факторного експерименту, треба, виходячи з виразу (5.8) для нормованого кроку, знайти значення у природних одиницях кроків варіювання іншими факторами. Воно буде

У цьому випадку одержимо координати точки К5 (першої точки), що лежить в напрямку градієнта.

Використовуючи співвідношення

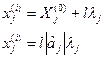(5.9)

одержані з виразів (5.5), (5.7) з урахуванням X _jcep=X_j⁽⁰⁾ i X_j⁽⁰⁾=0, можна знаходити координати точок, що лежать в напрямку градієнта, де l -крок просування в напрямку градієнта.

Приклад. За МКС визначити екстремальну область для функції відгуку.

На вхід об’єкта діють два фактори Х1 і Х2, для яких задано (в природних одиницях):

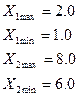
Визначимо координати базової точки і інтервали варіювання факторів:

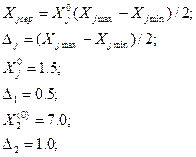
Таблиця 5.1

N	X1	X2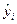
	-1	-1	95.0
	+1	-1	90.0
	-1	+1	85.0
	+1	+1	82.0

В околиці базової точки X _jcep=X_j⁽⁰⁾ згідно з матрицею планування ПФЕ провели експеримент і одержали значення вихідної величини (функція відгуку) у відповідно до табл. 5.1.

На основі формули 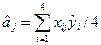знайдемо значення коефіцієнтів:

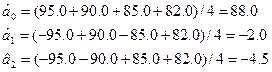
Таким чином, рівняння регресії, одержане в околиці базової точки X_j⁽⁰⁾ має вигляд

Найбільш суттєво впливає на зміну функції відгуку фактор Х₂, бо коефіцієнт при ньому за модулем найбільший.

Виберемо крок варіювання фактором Х₂, рівний λ₂=-0,5 (крок взято зі знаком «мінус», оскільки відшукується максимум, а збільшення значення Х₂ у вихідному рівнянні регресії приводить до зменшення оцінки вихідної величини.

Потім визначаємо нормований крок варіювання факторів в кодованій системі координат:

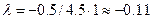
округлюємо до першої значущої цифри після коми λ=-0,1. Знаючи λ можна визначити крок варіювання фактором Х₁ у природних одиницях, що дозволить знайти координати першої точки в напрямку градієнта (аналогічно точці К5 на рис. 5.3).

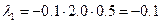
Тоді координати точки К₅ за умовою, що l =1 (перший крок просування до екстремуму) визначаються згідно з (5.9):

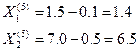
Встановивши значення Х₁=1,4 і Х₂=6,5 в результаті досліду одержимо значення функції відгуку Y(K₆).

Значення вихідної величини (вірніше, його оцінку) можна одержати на основі рівняння регресії, використовуючи вираз (5.9) для знаходження кодованих значень факторів при l =1:

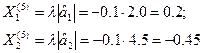
Тоді

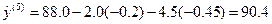
У кожній робочій точці необов’язково проводити реальні досліди. Щоб зменшити обсяг досліджень, а значить, збільшити їх ефективність, частину натурних дослідів на об’єкті замінюють на так звані «у думці». «У думці» досліди полягають в одержанні значень вихідної величини на основі лінійного рівняння регресії при підстановці в нього координат робочої точки, визначених на основі виразу (5.9), як це було проведено вище.

Реальні перевірочні досліди проводять через два-три дослід «у думці». На рис. 5.4 зображений переріз поверхні відгуку вертикальною площиною, слід якої проходить через промінь К₀М. «Ідеальна» крива 1 являє собою дійсний переріз поверхні відгуку, а пряма 2 – значення вихідної величини, одержані (передбачені) на основі лінійного рівняння регресії.

Рис. 5.4 - Розріз поверхні відгуку в напрямку крутого сходження

Перший цикл крутого сходження припиняється після проходженнячасткового екстремуму (точка К₈), про що вирішують за реальними дослідами. Тому в міру наближення до час ткового екстремуму необхідно частіше проводити перевірочні досліди, а після проходження часткового екстремуму в ряді випадків поставити допоміжний перевірочний дослід у проміжках між тими двома робочими точками, після яких почалося зменшення вихідної величини і в яких досягнуті приблизно однакові й найбільш із всіх попередніх значень Y. Крім того, як видно з рис. 5.4, про проходження області час ткового екстремуму свідчить зміна знаку різниці між обчисленими і дослідними даними (дослідами «у думці» й натуральними). Другий цикл починається з досягнутої точки час ткового екстремуму, прийнятої за нову базову точку, в околицях якої ставиться ПФЕ або ДФE.

У міру наближення до екстремальної області крок варіювання необхіднозменшити. Одержана нова лінійна модель дає новий напрямок градієнта вздовж якого проводяться досліди «у думці» і перевірочні до досягнення в данному напрямку часткового екстремуму.

Свідченням досягнення глобального екстремуму є неадекватність лінійної моделі, одержаної на основі ПФЕ або ДФE, коли коефіцієнти при парних взаємодіях різко зростають.

Розглянемо приклад застосування методу крутого сходження при визначенні екстремальної (максимальної) області. Функція відгуку 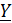залежить від семи факторів, граничне значення яких вибиралось на баз і накопиченого раніше досліду. Вихідні дані, матриця планування, результати дослідів для пробних точок, координати кроків варіювання при просуванні до екстремуму і значення функції відгуку в цих точках зведені в табл. 5.2.

Для визначення напрямку градієнта в околиці базової точки з рівнем X_j⁽⁰⁾ достатньо в її околиці побудувати лінійну регресійну модель, що апроксимуєповерхню відгуку:

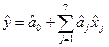
коефіцієнти якої пропорційні проекціям градієнта. Для цієї мети дос татньо провести N≥8 дослідів. Таким чином, в околиці базової точки достатньо провести ДФE виду 2 ^7-4, в якому фактори х₁, х₂, х₃ вважаються основними і для яких матриця плану базується за відомим правилом, як при ПФЕ.

Рівні варіювання допоміжних факторів встановлюють на основі чотирьох генеруючих співвідношень, яким відповідають визначаючі контрасти.

Нехай були вибрані такі ГС:

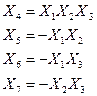
що дають відповіді ВК:

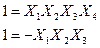
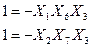
В узагальнюючий визначальний контраст будуть входити вихідні ВК, а також їх сполучення по 2, по 3 і одне сполучення з усіх чотирьох ВК. Загальне число сполучень, які входять у ВК, складає 4+6+4+1=15 і дає дуже складну картину змішування оцінок коефіцієнтів. Проте змішування оцінок визначати не треба, оскільки мета пробних дослідів при МКС - це визначення напрямку градієнта, тобто оцінка коефіцієнтів 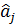при факторах згідно з матрицею ДФЕ виду 2 ^7-4. При вибраних ГС були проведені досліди і одержані значення функції відгуку в точках плану. Виходячи з формули

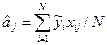
Знайдені оцінки коефіцієнтів і рівняння регресії:

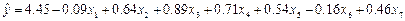
Найбільш суттєвим є фактор Х₃, оскілки коефіцієнт 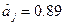за модулем є найбільшим з усієї сукупності

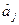. Для нього встановлюємо крок варіювання, наприклад Х₃=0,02.

Тоді згідно з (5.8) нормований крок варіювання:

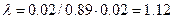
звідки відповідно до виразу 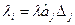знайдемо обчисленні значення кроку варіювання вхідними величинами у природній системі координат, що дозволить одержати координати точок, які лежать в напрямку градієнта. Так, дав змінної Х₁ робочий крок варіювання

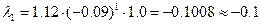
Аналогічно визначаються й інші 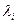(результати записані у відповідний рядок таблиці).

При крутому сходженні немає необхіднос ті проводити реально всі дослідження – їх можна замінити на «у думці». Для цього на основі співвідношення (5.9) визначають значення Х_j і розраховують значення .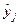

Таблиця 5.2

Група даних	Впливаючі величини (фактори)	X1	X2	X3	X4	X5	X6	X7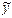
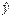
Вхідні дані для експерименту	Базовий рівень	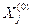	0.1	0.02		0.1	0.4	0.4	-	-
Інтервал варіювання	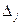	0.1	0.02		0.1	0.1	0.1	-	-
Нижчий рівень	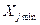					0.3	0.3	-	-
Верхній рівень	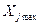	0.2	0.04		0.2	0.5	0.5	-	-
	Кодування з врахуванням генеруючи співвдношень	X1	X2	X3	X1 X2 X3	-X1 X2	-X1 X3	-X3 X2	-	-
Матриця плану ДФЕ		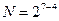	-1	-1	-1	-1	-1	-1	-1	1.5	1.5
	+1	-1	-1	+1	+1	+1	-1	3.5	3.5
	-1	+1	-1	+1	+1	-1	+1	6.2	6.2
	+1	+1	-1	-1	-1	+1	+1	3.2	3.2
	-1	-1	+1	+1	-1	+1	+1	5.3	5.3
	+1	-1	+1	-1	+1	-1	+1	5.1	5.1
	-1	+1	+1	-1	+1	+1	-1	5.3	5.32
	+1	+1	+1	+1	-1	-1	-1	5.8	5.8
Вхідні дані МКВ	Оцінка коеф.	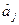№ досл.	-0.09	0.64	0.89	0.71	0.54	-0.16	0.46	-	-
Робочий крок	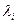-0.1	0.07	0.02	0.8	0.06	-0.02	-0.05	-	-
Круте сходження (досліди)	Удумці		1.9	0.17	0.04	4.8	0.16	0.38	0.45	-	6.95
Удумці		1.8	0.24	0.06	5.6	0.22	0.36	0.50	-	9.34
Удумці		1.7	0.31	0.08	6.4	0.28	0.34	0.55	-	12.65
Удумці		1.6	0.38	0.10	7.2	0.34	0.32	0.60	-	15.51
Натуральний		1.5	0.45	0.12	8.0	0.40	0.30	0.65	10.3	16.67
Натуральний		1.4	0.52	0.14	8.8	0.46	0.28	0.70	10.5	-
Натуральний		1.3	0.59	0.16	9.6	0.52	0.26	0.75	11.0	-
Натуральний		1.2	0.66	0.18	10.4	0.58	0.24	0.80	11.5	-
Натуральний		1.1	0.73	0.20	11.2	0.64	0.22	0.85	11.2	-
Натуральний		1.0	0.80	0.22	12.0	0.70	0.20	0.90	10.1	-

Так, для першого досліду «у думці» розраховані значення вихідної величини:

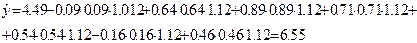Аналогічно знайдемо значення вихідної величини для точок у напрямку градієнта, в яких проводяться досліди «у думці», і занесемо в таблицю. Як вже відмічалося, на початковому етапі пошуку екстремуму натурний (реальний) дослід можна ставити через три – п’ять «у думці» і одержані значення 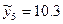порівняти з обчисленим 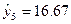. Згідно з рис. 5.3 можна припустити, що область екс тремуму вже пройдена, тому що , тобто обчислене значення більше реального. Тому наступний (шостий) дослід також необхідно провести натурним, щоб уточнити область екстремуму. Шостий дослід свідчить, що область екстремуму ще не досягнута, бо 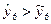. Таким чином, той факт, що в п’ятому досліді обчислені значення 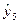більше дослідного значення 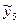можна пояснити тільки тим, що рівняння регресії добре апроксимує поверхню відгуку лише в області базової точки (про це можна судити при співпаданні обчислених і дослідних даних при реалізації ДФЕ 2 ^7-4). Це виходить із того, що ДФЕ 2 ^7-4 дає змішування оцінок, тому лінія регресії у всіх точках буде давати значення функції відгуку більше, ніж в експериментальних даних (на рис. 5.3 ця ситуація представлена пунктирною лінією). У подальшому проводимо тільки натурні досліди. Оскільки значення вихідної величини, одержане в шостому досліді, буде більше значень, одержаних в сьомому, а також дев’ятому і десятому дослідах, то точка восьмого досліду знаходиться в облас ті час ткового екстремуму в знайденому за ДФЄ 2 ^7-4 напрямку градієнта.

На цьому закінчується перший цикл крутого сходження, із розгляду якого випливає, що навіть за один цикл досягнуто функцію відгуку

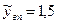(), яке в 2,5 раза перевершує значення в базовій точці 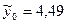, що свідчить про ефективність МКС.

Після досягнення облас ті екстремуму проводять її дослідження. Для цієї цілі будують плани більш високого порядку, оскільки поверхня поблизу екстремуму погано апроксимується гіперплощиною.

Як вже відмічалось, про досягнення екстремальної області свідчить зменшення за абсолютною величиною коефіцієнтів при факторах і різке зростання коефіцієнтів моделі, одержаної на основі ПФЕ або ДФЕ в області поточної базової точки.

Date: 2015-09-19; view: 528; Нарушение авторских прав