
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Повний факторний експеримент. У факторних експериментах на відміну від класичних відбуваються одночасно варіювання всіма незалежними змінними
|
|
У факторних експериментах на відміну від класичних відбуваються одночасно варіювання всіма незалежними змінними. Експеримент, у результаті якого всі незалежні змінні варіюються на всіх вибраних рівнях, називається повним факторним експериментом (ПФЕ).
Кількіс ть дослідів при ПФЕ підраховується так:
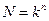
де – k – кількість рівнів, n – число факторів.
Оскільки фактори різні за фізичною природою і змінюються в різних динамічних діапазонах, для подальшої формалізації процесу аналізу і незалежності одержаних результатів від зміни масштабу вхідних величин фактори попередньо кодують. Для цього використовують співвідношення:
max i сс i min
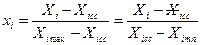 (4.1)
(4.1)
де 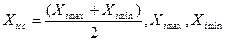 - граничні значення у рівняннях незалежних змінних.
- граничні значення у рівняннях незалежних змінних.
Таким чином операція кодування незалежних змінних обчислюється в перенос і центру координат в точку x i ср, що називається в подальшому центром плану експерименту
У кодованій системі на основі (4.1) будуть додержуватись відповідності:
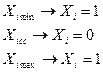
У подальшому будуть використовуватися кодовані змінні.
У разі парної залежнос ті для визначення лінії регресії достатньо провести два досліди при граничних значеннях фактора x1, тобто план експерименту має вигляд 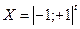 . Якщо число вхідних величин дві – x1і x2, тобто реалізується двох факторний експеримент, то для побудови матриці плану повного факторного експерименту, який дозволяє оцінити коефіцієнти моделі y=a0+a1x1+a2x2, необхідно користуватись нас тупним правилом: при додаванні нового фактора кожна комбінація рівнів вихідного плану зустрічається двічі - в сполученні з нижнім (-1) і верхнім (+1) рівнями нового фактора. Іншими словами, матриці вихідного плану (однофакторного експерименту) треба повторити двічі – при нижньому рівні (x2=-1) і верхньому рівні (x2=+1) доданого фактора. Виходячи з цього, правила, можна побудувати і матрицю плану і трифакторного експерименту.
. Якщо число вхідних величин дві – x1і x2, тобто реалізується двох факторний експеримент, то для побудови матриці плану повного факторного експерименту, який дозволяє оцінити коефіцієнти моделі y=a0+a1x1+a2x2, необхідно користуватись нас тупним правилом: при додаванні нового фактора кожна комбінація рівнів вихідного плану зустрічається двічі - в сполученні з нижнім (-1) і верхнім (+1) рівнями нового фактора. Іншими словами, матриці вихідного плану (однофакторного експерименту) треба повторити двічі – при нижньому рівні (x2=-1) і верхньому рівні (x2=+1) доданого фактора. Виходячи з цього, правила, можна побудувати і матрицю плану і трифакторного експерименту.
У табл. 4.3 показана поетапна побудова матриці плану в міру збільшення числа факторів.
Таблиця 4.3
| № п/п | X1 | X2 | X3 | № п/п | X1 | X2 | X3 |
| -1 | -1 | -1 | -1 | -1 | +1 | ||
| +1 | -1 | -1 | +1 | -1 | +1 | ||
| -1 | +1 | -1 | -1 | +1 | +1 | ||
| +1 | +1 | -1 | +1 | +1 | +1 |
Якщо розглянути матрицю дво факторного експерименту, побудованого за прийнятим вище правилом, то видно, що в ній присутні всі N=22=4 сполучення факторів
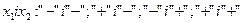
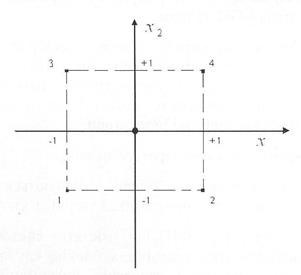
Рис. 4.1 - Розташування точок за ПФЕ 2n у факторній площині
Геометричний план такого експерименту інтерпретується точками, розташованими у вершинах квадрату.
Побудована таким чином матриця має ряд важливих якостей:
1) ортогональніс ть, що забезпечує незалежність оцінок коефіцієнтів моделі:
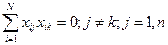
де j, k =1, n =- номери вектор-стовпців відповідних факторів; i – плинна точка факторного простору, в якому проводиться експеримент. Іншими словами, дану властивість можна сформулювати так: скалярний добуток вектор-стовбців матриці планування дорівнює нулю;
2) симетричність, що забезпечує незалежність вільного числа:
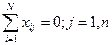
тобто сума елементів вектор-стовпців xj дорівнює нулю, точки, в яких проводяться досліди, розташовані симетрично по відношенню до центру плану;
3) нормування, що забезпечує однакову дисперсію оцінки коефіцієнтів:
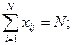
Остання рівність випливає із того, що кодовані фактори набувають тільки значення 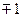 .
.
Розрахунок і статис тична оцінка коефіцієнтів рівняння регресії, одержаного на основі плану ПФЕ, засновані, як і при пасивному експерименті, на застосуванні регресійного аналізу. З огляду на те, що матриця плану має властивості ортогональності, всі розрахунки дуже спрощуються. Це зумовлено тим, коваріаційна матриця C -1 у виразі для визначення оцінок коефіцієнтів
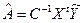
виявляється діагональною, що приводить до системи незалежних оцінок коефіцієнтів рівняння регресії:
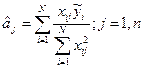 (4.2)
(4.2)
Кожний коефіцієнт розраховується незалежно від інших, причому загальне число коефіцієнтів не повинно перевищувати числа рівнянь, з яких вони визначались, а це число співпадає з числом рядків матриці планування, що визначається співвідношенням N =2 n. Згідно з властивістю нормування матриці плану повного факторного експерименту вираз для визначення оцінки коефіцієнта рівняння регресії при дворівневому експерименті остаточно запишеться у вигляді
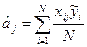 (4.3)
(4.3)
Так, якщо відповідно до матриці плану дво факторного експерименту були одержані вихідні величини
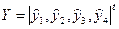 ,то оцінки коефіцієнтів при факторах запишуться так:
,то оцінки коефіцієнтів при факторах запишуться так:
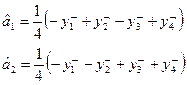
Отже значення 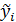 одержане в результаті проведення досліду в i- й точці факторного простору (згідно з i- м рядком матриці плану), береться зі знаком, відповідним знаку рівня вимірювання j-го фактора, коефіцієнт при якому обчислюється для даного i- го рядка матриці планування. Так,
одержане в результаті проведення досліду в i- й точці факторного простору (згідно з i- м рядком матриці плану), береться зі знаком, відповідним знаку рівня вимірювання j-го фактора, коефіцієнт при якому обчислюється для даного i- го рядка матриці планування. Так,
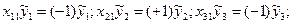 і т.д.
і т.д.
Таблиця 4.4
| № п/п | X0 | X1 | X2 | X1 X2 | yi |
| +1 | -1 | -1 | +1 | y1 | |
| +1 | +1 | -1 | -1 | y2 | |
| +1 | -1 | +1 | -1 | y3 | |
| +1 | +1 | +1 | +1 | y4 |
Якщо в кожній точці факторного простору дослід проводиться m раз,то
вираз (4.3) зміниться:
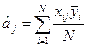 (4.4)
(4.4)
де  - “середнє рядкове” значення вихідної величини об'єкта
- “середнє рядкове” значення вихідної величини об'єкта
в і-му рядку матриці плану.
Для визначення оцінки коефіцієнта a0 необхідно матрицю плану доповнити вектор-стовпчиком фіктивної змінної х0, тотожньо, рівній одиниці, як це показано в табл. 4.4.
Зважаючи на те, що вектор-стовпчик матриці плану задовольняє умові симетричності, то
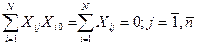
Таким чином, вектор-стовпчик фіктивної змінної буде ортогональним вектор-стовпчикам незалежних змінних, тому оцінка вільного члена буде визначатися незалежно від оцінок 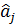 відповідно до виразу (4.3):
відповідно до виразу (4.3):
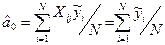
Якщо модель містить лінійні парні взаємодії, факторів хјхk, то для визначення оцінок коефіцієнтів при них матриця плану доповнюється вектор-стовпчиком для взаємодії. Причому чергування знаків у цьому векторі-стовпчику одержують шляхом перемножування знаків вектор-стовпчика хј хk.
У табл. 4.4 показана процедура визначення оцінки коефіцієнта a12 при взаємодії х1 х2.Отриманий таким чином вектор-стовпчик буде мати три перелічені властивості матриці планування - ортогональніс ть, симетричність і нормування. Таким чином, оцінка коефіцієнта при лінійній взаємодії знаходиться незалежно на основі того ж виразу (4.3):
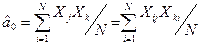
Знайдені таким чином оцінки коефіцієнтів моделі показують ступінь впливу факторів і їх взаємодії на вихідну величину. Якщо перед коефіцієнтом стоїть знак плюс, то із збільшенням даного фактора вихідна величина збільшується, а якщо знак мінус, то навпаки.
Date: 2015-09-19; view: 510; Нарушение авторских прав