Нелінійна регресія

До цього часу ми вважали, що математична модель, яка описує поведінку об’єму, який досліджується, лінійна і може бути предс тавлена у вигляді

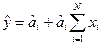
Проте уявлення про вид взаємозв’язку між величинами може бути невірним. Щоб підтвердити достовірність результатів, необхідно оцінити відхилення розрахованих значень вихідної величини, одержаних за результатами експерименту (спостережень), з цими експериментальними даними тобто оцінити величину, пропорційну Σ(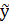 I_і – ŷ_і)2. Але для цього треба виконати спочатку вагому процедуру визначення оцінок коефіцієнтів â, а потім, в гіршому випадку, пересвідчитись, що гіпотеза про вигляд моделі булла вибрана невірно.

Можливий більш швидкий шлях оцінки відхилення залежнос ті від лінійної. Він базується на визначенні коефіцієнтів детермінації (дисперсійного або кореляційного відношень). Розглянемо поле кореляції для парної залежності (див. рис. 3.5) і побудуємо в ньому лінію регресії, що задовольняє методу найменших квадратів. Для довільної точки з координатами(х_i, у_i) розглянемо повне відхилення вихідної величини від середнього значення (центру тяжіння). Відповідно до рис. 3.5 для даної і-ї точки можна записати

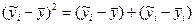
Віднесемо в квадрат

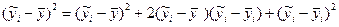
Для всієї сукупності точок поля кореляції

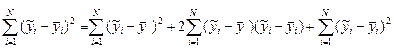
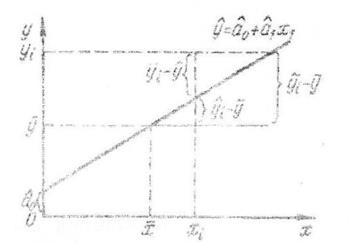
Рис. 3.5 - Побудова лінії регресії і визначення повної дисперсії вихідної величини

У разі некорельованості систематичних 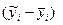і випадкових 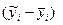відхилень друга в правій частині дорівнюватиме

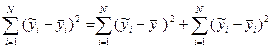(3.9)

Розділивши на (N-1), одержимо вираз для повної дисперсії вихідної величини, що складається із дисперсії умовного математичного очікування і середньої умовної дисперсії.

Перша складова у правій час тині характеризує розсіяння впливу вхідної величини, що досліджується, тобто є дисперсією, «що пояснюється», оскільки 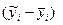залежить від рівняння регресії і, відповідно, зумовлено регресійним зв’язком. Відхилення 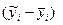варіюються випадковим чином і не можуть бути пояснені моделлю, тобто ці відхилення відображають вплив випадкових факторів. До випадкових в даному випадку відносяться невраховані фактори, а також високі ступені або комбінації врахованих факторів.

Із наведеної трактовки випливає, що дисперсія умовного математичного очікування може служити характеристикою ступеня зв’язку між вхідною і вихідними змінними, а умовна дисперсія характеристичного ступеня невизначеності, неідентичності, кількісно характеризується неадекватністю даної моделі через неврахування інших факторів моделі, крім х.

Коефіцієнт детермінації регрес ії визначиться як відношення суми квадратів пояснимих відхилень (дисперсії умовною математичного очікування) до всієї суми квадратів відхилень (дисперсії вихідної величини) виразу, тобто

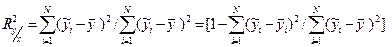
Із аналізу ос таннього виразу випливає, що 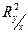прагне до одиниці, коли

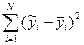прагне до 0. Це свідчить про те, що величини, які досліджуються, пов’язані функціональним зв’язком, а розкид вихідних величин yі пов’язаний, наприклад, із випадковою похибкою їх вимірювання.

Із цього ж виразу виходить, що коефіцієнт детермінації буде дорівнювати нулю тільки в тому разі, коли

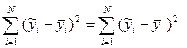
тобто коли розсіяння біля лінії регресії ŷі дорівнюють розсіянням біля загального середнього у при будь-якому х_і. Це може бути, якщо вхідна і вихідна величини незалежні.

Із цього випливає, що якщо вхідна і вихідна величини об’єкта що осліджується, незалежні, проте отримане твердження не завжди буде вірним. У загальному випадку коефіцієнт детермінації регресії лежить в межах

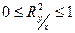
і інтерпретує кількісну характеристику міри невизначеності випадкової величини У за значеннями випадкової величини Х. На відміну від коефіцієнта кореляції, коефіцієнт детермінації несиметричний по відношенню до змінних, що досліджуються, тобто 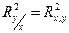. У регресіях з детермінованими незалежними змінними коефіцієнт детермінації необхідно трактувати тільки як показник, що відображає, наскільки модель регресії краще моделі середнього.

Взаємозв’язок між коефіцієнтами кореляції і детермінації залишається таким:

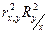(3.10)

Рівність тут виконується лише в тому випадку, коли є строга лінійна залежність У на Х, тобто ŷ = М [У/х]. Із нерівності виходить, що кількіснахарактеристика стохастичного зв’язку Х і У, виміряна коефіцієнтом детермінації, може бути більше нуля у випадку нульового коефіцієнта кореляції. Відомо, що коефіцієнт кореляції при двомірному нормальному розподілу має сенс тільки при лінійному зв’язку. Тому можна використовувати співвідношення між коефіцієнтами кореляції і детермінації, щоб оцінити правильність вибору лінійної моделі.

Розглянемо статис тику [С.А. Айвазян. Статистические исследования зависимости.-М.: Металлургия, 1968.-182с.]

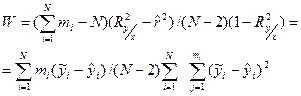
яка пропорційна сумі відхилень групових середніх yі від прямої регресії, поділеної на суму відхилень yіj від загального середнього. Вона має F - розподіл Фішера з f₁=(N-2) i f₂=(Σm_i-N) ступенями свободи. Тут N - число точок (значень хі), в яких проводились досліди; mi - кратність проведення досліду в і-й точці, 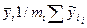- середнє значення вихідної величини, виміряне для і-ї точки, y =Σm_і /N – загальне середнє значення вихідної величини. Знайдене значення W порівнюється з табличним значенням Fт при вибраному рівні статистичної значущості а і числі с тупенів свободи f₁ i f₂. Якщо W>F_т, то гіпотеза про лінійність зв’язку між вхідною і вихідною величинами з вибраним рівнем статистичної значущості відкидається.

Переконавшись, що при статис тичній обробці результатів експерименту лінійна модель неадекватна об’єкту, що досліджується, або ж коли при графічному зображенні поля кореляції видно, що залежність явно нелінійна, необхідно висунути гіпотезу, наприклад при однофакторному експерименті, про квадратичну парну залежніс ть вигляду

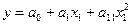
При цьому слід пам’ятати, що мова йде про нелінійну залежність за факторами, але лінійну за параметрами. Одержати оцінки коефіцієнтів парної квадратичної регресії можна на основі системи нормальних рівнянь для множинного лінійного регресійного аналізу, підс тавивши d→d і лінійного

X₂→X₁², тобто

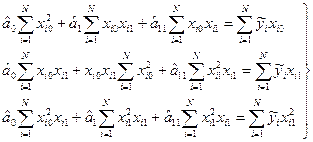
Вирішивши цю систему рівнянь, одержимо оцінку коефіцієнтів парної квадратичної моделі. Користуючись відомою властивістю системи нормальних рівнянь, можна записати систему рівнянь для одержання оцінок коефіцієнтів парної залежності будь-якого порядку. Проте при виконанні операцій зведення в ступінь для одержання формул порядку вище четвертого ступеня, похибки округлення стають нас тільки великими, що зводиться нанівець виграш від підвищення порядку регресії (про цю обставину не треба забувати).

Викладений вище підхід поширюється і на регресійний аналіз, коли модель містить фактори в другому й вище ступені.

Date: 2015-09-19; view: 914; Нарушение авторских прав