Результат і похибка опосередкованих вимірювань

Довірчі границі випадкової похибки і границі невилученої систематичної похибки результату опосередкованого вимірювання з нелінійною залежністю визначають за формулами, наведеними вище, підставляючи в останні замість коефіцієнтів 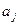відповідно перші похідні .

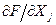Обчислюємо довірчу сумарну похибку результату опосередкованого вимірювання.

Результат опосередкованих вимірювань записується у вигляді

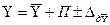при 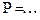, (1.54)

де - границі допустимої випадкової похибки опосередкованих вимірювань.

Формули (1.50), (1.51), (1.54) для оцінки СКВ і результату опосередкованих вимірювань справедливі за умови, що відомі оцінки дисперсії (і СКВ) початкових величин. Значення коефіцієнта 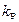визначається для заданої довірчої ймовірності P, виходячи із закону розподілу результату 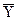опосередкованого вимірювання. Якщо закон розподілу результату 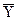опосередкованих вимірювань можна вважати нормальним, то для визначення 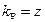(і довірчих границь 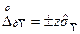) використовується інтегральна функція нормованого нормального розподілу при великому обсязі вимірювань 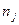. При малому обсязі 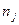нормально розподілених результатів спостережень 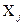слід користуватися розподілом Стьюдента з «ефективним» числом степенів вільності, що визначається виразом:

.

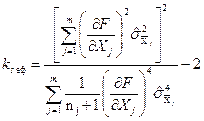Якщо кількість спостережень усіх аргументів однакові 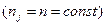, то:

.

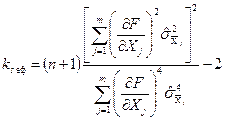При лінійній функціональній залежності опосередкованих вимірювань маємо 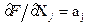і отримуємо приведені вище формули для ефективного числа степенів вільності .

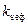Оскільки число 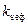здебільшого є дробовим, то для пошуку величини 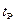за таблицею розподілу Стьюдента необхідно використовувати інтерполяцію.

Довірчі границі повної похибки опосередкованих вимірювань (із врахуванням випадкової і невилученої систематичної складових похибки вимірювань) знаходять за відповідною методикою [29].

Отже, загальна методика статистичної обробки результатів опосередкованих вимірювань передбачає наступний алгоритм:

1) вилучення відомих (виявлених) систематичних похибок з результатів вимірювань кожного аргументу;

2) перевірку відповідності реального розподілу результатів прямих вимірювань кожного аргументу нормальному закону за одним із критеріїв згоди. Якщо така відповідність підтверджується, то проводять перевірку грубих похибок і їх вилучення з результатів вимірювань;

3) обчислення оцінок аргументів та їх похибок;

4) перевірка відсутності кореляції між результатами вимірювань аргументів попарно, при її наявності обчислюють відповідні коефіцієнти кореляції;

5) обчислення результату опосередкованого вимірювання;

6) обчислення довірчої випадкової похибки і загальної похибки результату опосередкованого вимірювання; при нелінійній залежності знаходять систематичну похибку опосередкованих вимірювань, обумовлену перехресними членами.

При прямих одноразових вимірюваннях початкових величин 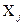процедура визначення результату Y опосередкованих вимірювань зберігається такою самою, як і при багаторазових вимірюваннях. Проте при прямих одноразових вимірюваннях початкових величин 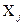для оцінки характеристик похибки опосередкованих вимірювань широко використовуються абсолютні і відносні значення похибок.

Формули обчислення абсолютних і відносних похибок опосередкованих вимірювань для тих функціональних залежностей, які часто зустрічаються на практиці, наведені в табл.1.2 Якщо похибки є систематичними, то формули в табл.1.16 використовують з урахуванням знаків похибок. Для випадкових похибок здійснюється підсумовування за модулем, тобто арифметичне сумування, причому за величину 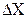беруть границі допустимих похибок (максимальні значення).

Табл.1.2 свідчить, що піднесення аргументу до цілого степеня значно збільшує, а добування цілого степеня аргументу зменшує похибки результату. Тому вимірювання величин, які у формулу (1.40) входять у вигляді 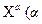- ціле додатне число), необхідно виконувати з більшою точністю, а вимірювання величин, які входять у формулу (1.40) у вигляді 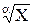, може здійснюватися з меншою точністю. Якщо результат опосередкованих вимірювань виражається через степеневу функцію аргументів, наприклад,

,

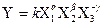то для відносної систематичної похибки отримаємо

,

а для оцінки «зверху», тобто максимального значення відносної випадкової похибки

.

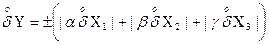Таблиця 1.2 – Формули обчислення абсолютних і відносних похибок опосередкованих вимірювань

Функції Y	Похибки
Абсолютна,	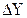Відносна,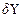

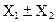
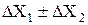
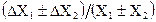
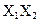
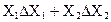
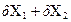
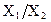
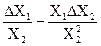
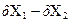
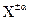
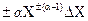
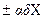
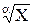
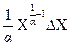
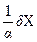
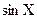
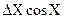
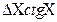
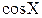
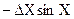
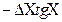
Проте така оцінка дає завищені результати і її застосування доцільно при 2 або 3 складових похибки. При більшому числі складових випадкової похибки опосередкованих вимірювань (за числом аргументів m), абсолютну випадкову похибку результату слід обчислювати за правилами сумування незалежних випадкових величин, тобто геометрично:

.

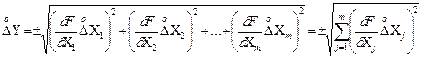Величину називають середнім квадратичним значенням абсолютної випадкової похибки опосередкованих вимірювань.

Тоді СКВ відносної випадкової похибки опосередкованих вимірювань:

.

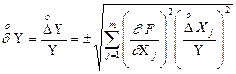При окремій оцінці систематичних і випадкових складових похибки результату опосередкованих вимірювань оцінити систематичну похибку результату неможливо, не знаючи оцінок систематичних похибок початкових величин 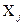. Але якщо вони відомі, то їх необхідно вилучити з результатів прямих вимірювань 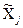, а потім оцінити результат опосередкованого вимірювання за цими виправленими значеннями 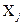. Водночас така оцінка систематичної похибки може бути проведена після закінчення експерименту. Тоді її у вигляді поправки необхідно врахувати в остаточному результаті опосередкованого вимірювання (1.54). Оцінка систематичної похибки може використовуватися також під час підготовки до експерименту як орієнтовна оцінка. Наприклад, якщо припустити, що похибка результату опосередкованого вимірювання визначається тільки похибкою ЗВТ при вимірюванні величин 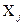, причому в цих ЗВТ переважаючою є систематична похибка (випадковою похибкою можна знехтувати), то на основі оцінки систематичної похибки при 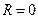(провівши формальну заміну 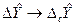, 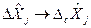) можна вибрати ЗВТ з такими границями допустимих систематичних похибок, щоб похибка результату опосередкованих вимірювань величини Y не перевищувала заданого значення [49].

Наведемо спрощений приклад опрацювання результатів опосередкованих вимірювань, де вихідними даними є формула зв'язку та масиви результатів спостережень, опрацьовані за методикою опрацювання результатів багаторазових прямих вимірювань:

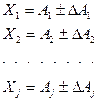(1.55)

Туг А_j — найвірогідніше значення j -го аргументу; ∆A_j — надійна межа загальної похибки результату прямого вимірювання цього аргументу.

Формула зв'язку:

Y=f(X_l, X₂,...,X_N). (1.56)

Метрологічна обробка результатів опосередкованих вимірювань полягає в обчисленні найвірогіднішого значення шуканої величини А_у.; для цього треба у формулу зв'язку підставити результати А_j - прямих вимірювань:

А_у=f(А_l, А₂,..., А_N). (1.57)

Спосіб обчислення надійних границь загальної похибки результату опосередкованого вимірювання залежить від характеру формули зв'язку.

Загальна похибка результату опосередкованого вимірювання визначається співвідношенням:

(1.58)

де Х_j - істинні значення аргументів; 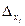- похибки вимірювань цих аргументів.

Формула (1.58) не застосовується на практиці. Якщо розкласти її в ряд Тейлора, матимемо:

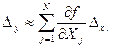. (1.59)

Тут df/dX_j - частинна похідна від Y по j -му аргументу; 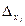- абсолютна похибка прямого вимірювання j -го аргументу.

В реальних умовах у випадку додавання похибок можлива їх часткова взаємна компенсація, тому така формула дає дещо завищені результати. Кращі результати можна отримати середньоквадратичним сумуванням похибок:

(1.60)

Величину D_j=(df/dХ_j) 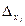називають частковою похибкою результату опосередкованого вимірювання.

Для функції однієї змінної Y=f(X) абсолютна похибка результату:

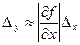. (1.61)

Якщо Y= Х^а, то ∆_у ≈а∙х^а-1∆_х; цей вираз зручніше подати у вигляді відносної похибки:

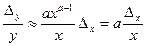. (1.62)

Якщо ж 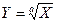, то 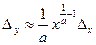; відносна похибка:

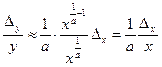. (1.63)

Для алгебраїчної суми Y= аХ₁ + bХ₂ +... абсолютна похибка результату:

.

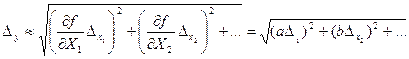(1.64)

Для добутку 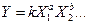відносна похибка результату:

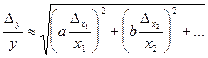(1.65)

У формулах (1.62), (1.65) величини k, a, b,... – це будь-які цілі або дробові, додатні або від'ємні числа.

Оскільки в результатах прямих вимірювань аргументів було використано надійні межі сумарних похибок, то похибки результатів опосередкованих вимірювань також відображують надійні границі сумарних похибок цих результатів.

Запис результату опосередкованого вимірювання має вигляд:

Y = A_y ± ∆A_у. (1.67)

Критерій незначних частинних похибок. Обчислюючи похибку опосередкованого вимірювання, доводиться сумувати частинні похибки, різні за значенням. Обчислення можна спростити, якщо знехтувати тими з них, значення яких неістотні порівняно з іншими.

Припустимо, треба підсумувати дві частинні похибки D₁ та D₂, причому D₁<<D₂. В загальному випадку сумарна похибка

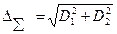(1.68)

Як відомо, похибка результату вимірювання округляється до однієї-двох значущих цифр; тому зміна правої частини виразу на 5 % практично не впливає на округлене значення 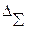, тобто нове значення:

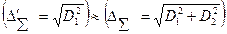
Отже, можна вважати, що

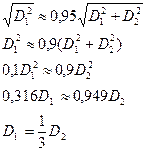(1.69)

Отже якщо серед двох частинних похибок одна відрізняється від іншої не менше, ніж утричі, то меншою з них можна знехтувати.

З критерію незначних частинних похибок випливає, що у випадку повірки вимірювальних приладів похибка зразкового приладу має бути принаймні втричі менша за похибку приладу, що повіряється.

Округлення констант. Визначаючи число значущих цифр у різних констант, що входять до формул зв'язку у випадку опосередкованих вимірювань, слід керуватися таким правилом: похибка округлення константи 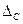має задовольняти нерівність

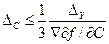(1.70)

де - задана похибка результату опосередкованого вимірювання; f - функція, що пов'язує константу С з вимірюваними величинами, причому константа умовно вважається незалежного змінною (аргументом).

При непрямих вимірюваннях величини X, функціонально пов'язаної з результатами прямих вимірювань величин Χ₁, Х₂ Х_з..., Х_n,похибки залежать від похибок величин Χ₁, Х₂ Х_з..., Х_n,. Це положення є справедливим як для випадкових, так і для систематичних похибок.

Для визначення похибки величини X використовують формулу:

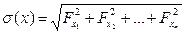, (1.71)

де 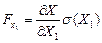; ;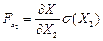..., 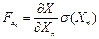– частинні

похідні X по Χ₁, Х₂ Х₃..., Х_n, σΧ₁), σ(Χ₂)..., σ(Χ_n) — середні квадратичні відхилення результатів вимірювання величин Χ₁, Х₂ Х₃..., Х_n в абсолютних одиницях.

Розглянемо застосування формули (1.189) на конкретних прикладах.

Нехай X = Х₁-Х₀ значення абсолютної похибки σ(Χ) = 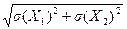або у відносній формі .

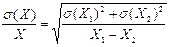Відповідно до теорії ймовірності, середнє квадратичне значення відхилення суми двох величин від її математичного сподівання:

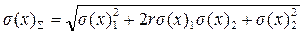, (1.72)

де σ (x)₁ і σ (x)₂ — відповідно середнє квадратичне відхилення додатків від їх математичного сподівання; r — коефіцієнт кореляції.

За ступенем корелятивності похибки поділяються на два види – сильнокорельовані (1> r >0,7) і слабкокорельовані (0< r < 0,7). Залежними сильнокорельованими похибками є такі, що зумовлені однією спільною причиною. Наприклад, якщо у вимірювальному пристрої є ряд підсилювачів із спільним джерелом живлення, то при збільшенні напруги живлення коефіцієнт підсилення всіх підсилювачів буде зростати, а при зменшенні – спадати. Виникаючі при цьому похибки окремих підсилювачів сильнокорельовані й підпорядковуються одному і тому самому закону розподілу. На практиці для сильнокорельованих похибок приймають r =1; в цьому випадку σ (x)_Σ = σ (x)₁ + σ (x)₂. Якщо у наведеному прикладі джерела живлення окремих підсилювачів незале­жні, то похибки підсилювачів не корельовані (r= 0) і їх слід підсумовувати геометрично як незалежні випадкові похибки:

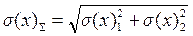. (1.73)

Похибку Δ (х)_с вимірювальної системи, що складається з k послідовно об'єднаних приладів (або перетворювачів), потрібно розглядати як ряд незалежних випадкових похибок і обчислювати на основі виразу (1.189):

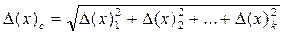, (1.74)

де (x)₁, (x)₂,...(х)_п - похибки окремих приладів. Точність вимірювання подається регламентованими способами виразу точності вимірювань.

Date: 2015-09-19; view: 688; Нарушение авторских прав