Гіпотези про параметри розподілу. Виникнення помилок першого та другого роду. Визначення обсягу випробувань

Критерії бувають параметричні і непараметричні. Параметричні критерії передбачають нормальний розподіл і пов’язані з обчисленням оцінок параметрів.

Гіпотеза про середнє значення нормального розподілу при відомому СКВ. Припустимо, що генеральна сукупність має нормальний розподіл, СКВ якого відоме. При рівні значущості α потрібно перевірити гіпотезу H ₀: v = v ₀. Альтернативна гіпотеза H₁ може бути

H ₁: v < v ₀; H ₁: v > v ₀; або H ₁: v ≠ v ₀.

Як статистику використовують випадкову величину

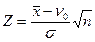(2.1)

що має нормований розподіл.

Критичну область визначають за допомогою таблиці нормального розподілу. Якщо альтернативна гіпотеза має вигляд H ₁: v < v ₀, використовують лівобічну критичну область, що задовольняє умову

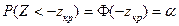(2.2)

Звідси випливає, що критична область – це множина таких Z, для яких Z<-z_кр (рис..2.2, а).

Якщо альтернативна гіпотеза має вигляд H ₁: v > v ₀, використовують правобічну критичну область, що задовольняє умову

Із таблиці знаходять значення z_кр з огляду на те, що

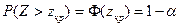
Знаходять критичну область Z>z_кр (рис. 2.2, б).

При альтернативній гіпотезі H ₁: v ≠ v ₀ використовують двобічну критичну область, що задовольняє умову

або

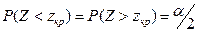
За таблицями знаходять Ф(z_кр)=1- α/2. У цьому разі критична область 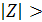z_кр (рис. 2.2, в).

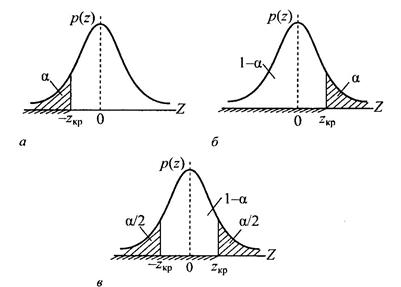
Рис. 2.2

Гіпотеза про середнє значення нормального розподілу при невідомому СКВ. Припущення аналогічні розглянутим раніше. У разі, коли СКВ невідоме, використовують випадкову величину (статистику Т)

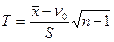(2.3)

яка має розподіл Стьюдента із кількістю ступенів свободи n-1.

Критичні області визначають так само, як і в попередньому випадку. Використання таблиць t-розподілу Стьюдента простіше, оскільки вони складені саме для визначення критичних областей.

Гіпотеза про дисперсії нормального розподілу. Припустимо, що генеральна сукупність має нормальний розподіл, де СКВ невідоме. Дисперсію визначають за результатами експерименту, що складається з n дослідів.

Висувають гіпотезу H ₀: σ²= 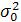. Як статистику використовують випадкову величину

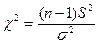(2.4)

яка має χ²-розподіл Пірсона із кількістю ступенів свободи n-1.

Вибір критичної області визначають залежно від обраної альтернативної гіпотези H ₁ та рівня статистичної значущості α, для чого за таблицями χ² визначають критичні значення обраної статистики.

Якщо альтернативна гіпотеза має вигляд H₁: σ²< 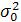, можна записати

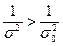
або з використанням виразу (2.4):

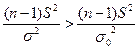
Для перевірки гіпотези варто використовувати правобічну критичну область (рис. 2.3, а).

При альтернативній гіпотезі H₁: σ²> 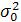, міркуючи аналогічно, виходять з умови

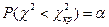
Ураховуючи особливості складання таблиці χ²-розподілу, значення 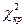знаходять згідно з умовою

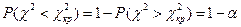
У цьому разі використовують лівобічну критичну область (рис. 2.3, б).

При альтернативній гіпотезі H₁: σ²≠ 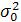знаходять двобічну (рис. 2.3, в) критичну область згідно з умовою

Зазвичай приймають симетричну за ймовірністю критичну оюласть, що задовольняє умову

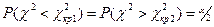
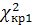Відповідно до цієї умови з таблиці можна безпосередньо знайти , а для визначення необхідно, як у попередньому випадку, використати умову:

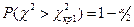
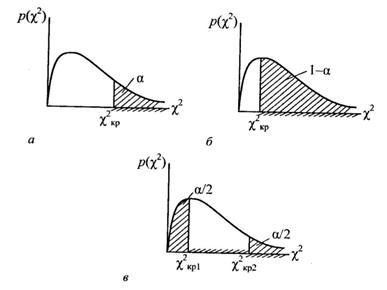
Рис. 2.3

Перевірка гіпотези про належність вибірки до генеральної сукупності. Як уже було розглянуто, помилкове рішення залежить від розмірів критичної області. З одного боку, чим менший розмір критичної області, тим частіше буде прийматися висунута гіпотеза H₀, але з другого боку, критерій втрачатиме чутливість стосовно альтернативної гіпотези.

Припустимо, на вхід приладу може бути подано одне з двох значень величин v₀ або v₁. При багаторазовому вимірюванні вихідної величини отримано значення х_і (і=1,…, n) та обчислено середнє 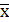(рис. 2.4). необхідно визначити, чи є 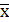оцінкою випадкової величини із центром v₀ або v₁. Висуваємо гіпотезу H ₀: 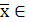v₀ при альтернативній гіпотезі H 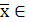₁: v₁.

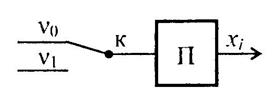
Рис. 2.4

Оскільки обсяг експериментальних даних обмежений, можливі обчислювані середні значення для даної вибірки будуть відповідно розсіяні навколо v₀ і v₁ (рис. 2.5).

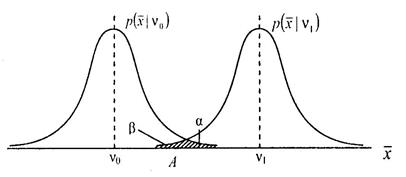
Рис. 2.5

Зважаючи на те, що середні значення мають нормальний розподіл, в інтервалі v₀, v₁ спостерігатиметься перекриття законів розподілу, а отже, і неоднозначність прийнятих рішень, що виражається в їхній можливій помилковості. Граничним значенням 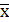, що відокремлює гіпотези H ₀, H ₁, є А. Якщо 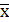буде ліворуч від А, то приймають гіпотезу H ₀, а якщо праворуч, – гіпотезу H ₁. Через перекриття законів розподілу для гіпотези H ₀ буде мати місце помилка першого роду, тобто буде прийматися гіпотеза H ₁, тоді як має місце гіпотеза H ₀. Таким чином, відхилення 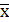у більший бік від А може бути викликане впливом випадкових факторів та обмеженим обсягом вибірки, а не належністю до v₁.

Імовірність виникнення помилки першого роду

де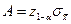

або

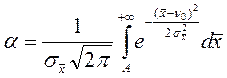
Крім помилки першого роду може виникнути й помилка другого роду, яка полягає в тому, що справджується гіпотеза H ₁, а обчислене середнє значення виявилося ліворуч А, тобто буде хибно прийматися гіпотеза H ₀.

Імовірність виникнення помилки другого роду:

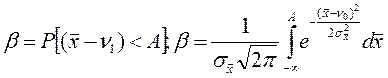
Визначення необхідного обсягу випробувань. Помилки першого та другого роду при фіксованих значеннях v₀, v₁ визначаються обсягом випробувань. Чим більший обсяг випробувань, тим ближче будуть групуватися можливі значення 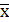до v₀ або v₁, а отже, зменшуватиметься область перекриття законів розподілів, тобто імовірність помилкових рішень (див. рис. 2.5).

Виходячи з оптимальності процедури перевірки гіпотез, необхідно визначити мінімальний обсяг випробувань, який забезпечує помилки першого та другого роду, що не перевищують заданих значень.

Нехай є два невідомі α і β (див. рис. 15.4), які є визначальними для встановлення мінімального обсягу. Крім того, α і β залежать від вихідного розсіювання σ, визначеного на підставі заздалегідь проведених досліджень, відстані між центрами розподілів v₀ і v₁ та вибору граничного значення А між ознаками (статистичними характеристиками).

Припустимо, що v₀, v₁; А; σ, β – задані. Оскільки є два невідомі значення α і β, а обсяг мінімальної кількості випробувань одночасно залежить від цих ймовірностей, необхідно скласти систему з двох рівнянь.

Для гіпотези H ₀ (рис. 2.6) можна записати:

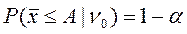
де А – фіксоване значення, при якому необхідно забезпечити одночасно значення α і β, менші від заданих.

У цьому разі застосовують статистику

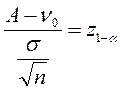
Графічну інтерпретацію співвідношення (2.5) наведено на рис. 2.6.

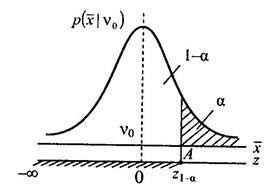
Рис. 2.6

Для гіпотези H ₁ (рис. 2.7) має виконуватися співвідношення

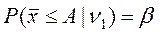
У цьому разі використовують статистику

(2.5)

Графічну інтерпретацію співвідношення (2.5) наведено на рис. 2.7.

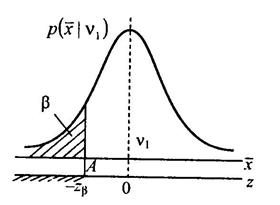
Рис. 2.7

Із виразу (15.3) знаходимо:

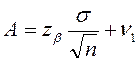
Підставляючи знайдене значення А у вираз (15.2), дістаємо:

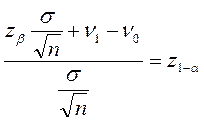
Після перетворення маємо:

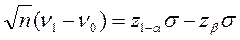
звідки кількість випробувань

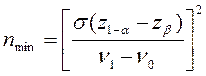(2.6)

Якщо границя А задана, обчислену кількість випробувань n округлюють до цілого числа в більшу сторону.

Можна, використавши ту саму систему рівнянь, визначити границю А, якщо заданий обсяг вибірки.

Питання для самоперевірки

1. Які критерії називаються параметричними?

2. Як перевіряється гіпотеза про середнє значення з відомим СКВ?

3. Як перевіряється гіпотеза про середнє значення з невідомим СКВ?

4. Як перевіряється гіпотеза про дисперсії?

5. Як перевіряється гіпотеза про наявність зсуву?

6. Як обчислюється ймовірність помилки першого роду?

7. Як обчислюється ймовірність помилки другого роду?

8. Що характеризує параметр А при визначенні необхідного обсягу випробувань?

9. Як обчислюється необхідний обсяг випробувань?